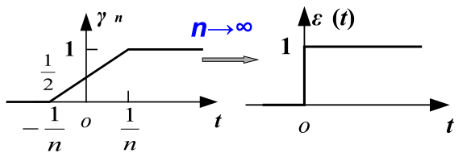
阶跃函数¶
用函数序列极限来定义
\[ \varepsilon(t) := \lim_{n \to \infty} \gamma_n(t) = \left\{\begin{matrix} 0, &t<0 \\ 1, &t>0 \end{matrix}\right. \]
它是一个奇异函数。
性质¶
\[ \int_{-\infty}^{t}\varepsilon(\tau)\mathrm{d}\tau=t\varepsilon(t) \]
\[ \int_{-\infty}^{t}\varepsilon(\tau)\varphi(\tau)\mathrm{d}\tau=\varepsilon(t)\int_{0}^{t}\varphi(\tau)\mathrm{d}\tau \]
广义函数¶
用 广义函数 定义
\[ \int_{-\infty}^{+\infty }\varepsilon(t)\varphi(t) \mathrm{d}t=\int_{0}^{+\infty }\varphi(t) \mathrm{d}t \]
与冲激函数的关系¶
是 冲激函数 的积分
\[ \varepsilon(t)=\int_{-\infty}^{t}\delta(\tau)\mathrm{d}\tau \]
相关文章