法线和切线¶

G-buffer 法线编码¶

如果将法线的 XYZ 分量直接存进 R8G8B8A8 G-buffer 的 RGB 通道中，会损失很多精度，光照结果有明显的瑕疵。

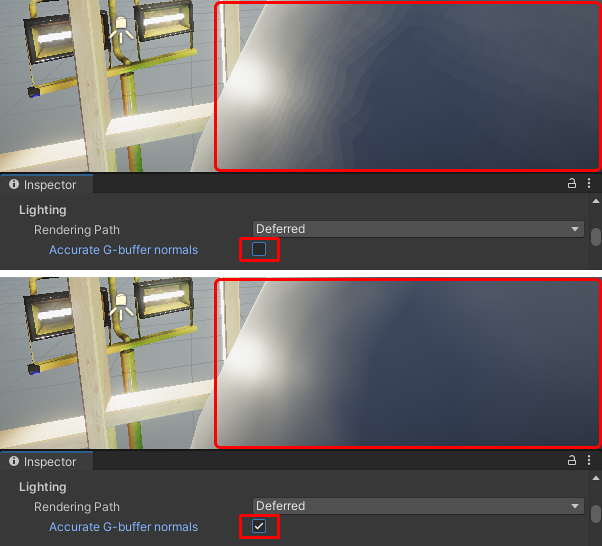
Accurate G-buffer normals, visual difference between the two options.

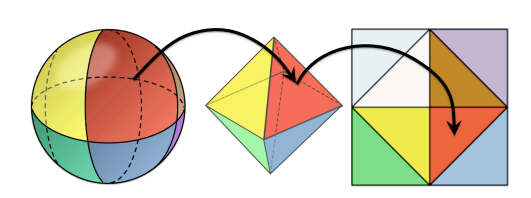
在 Unity 中启用 Accurate G-buffer normals 会切换到八面体（Octahedron）编码，提高法线的准确度，代价是增加了一点计算量。流程是

法线是一个单位向量，可以看成单位球上的点
将单位球上的点都投影到八面体上
将八面体投影到正方形上
将正方形坐标范围变为 \([0,1]^2\)，将坐标存进 G-buffer

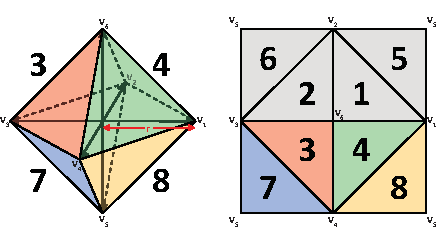
八面体的上半部分投影在正方形内部，下半部分投影在正方形四个角上。

八面体的方程为

它的中心为 \((0,0,0)\)，外接圆半径为 \(1\)。将任意一点 \((x,y,z)\) 投影到八面体的表面得到

\[ (x',y',z')=\left ( \frac{x}{\left | x \right |+\left | y \right |+\left | z \right |},\frac{y}{\left | x \right |+\left | y \right |+\left | z \right |},\frac{z}{\left | x \right |+\left | y \right |+\left | z \right |} \right ) \]

假设竖着的是 \(z\) 轴，接下来把点投影到正方形上

如果 \(z' \ge 0\)，点被投影到正方形内部，直接使用 \((x',y')\) 就行
如果 \(z'<0\)，点被投影到正方形四个角上，方法不唯一，常用的是
```
float2 output = (1.0 - abs(input.xy)) * sign(input.xy);
```

最后把 output 从 \([-1,1]^2\) 变成 \([0,1]^2\) 就能存进 G-buffer 了。

// Ref: https://github.com/Unity-Technologies/Graphics/blob/master/Packages/com.unity.render-pipelines.core/ShaderLibrary/Packing.hlsl

// Ref: http://jcgt.org/published/0003/02/01/paper.pdf "A Survey of Efficient Representations for Independent Unit Vectors"
// Encode with Oct, this function work with any size of output
// return float between [-1, 1]
float2 PackNormalOctQuadEncode(float3 n)
{
    //float l1norm    = dot(abs(n), 1.0);
    //float2 res0     = n.xy * (1.0 / l1norm);

    //float2 val      = 1.0 - abs(res0.yx);
    //return (n.zz < float2(0.0, 0.0) ? (res0 >= 0.0 ? val : -val) : res0);

    // Optimized version of above code:
    n *= rcp(max(dot(abs(n), 1.0), 1e-6));
    float t = saturate(-n.z);
    return n.xy + float2(n.x >= 0.0 ? t : -t, n.y >= 0.0 ? t : -t);
}

float3 UnpackNormalOctQuadEncode(float2 f)
{
    // NOTE: Do NOT use abs() in this line. It causes miscompilations. (UUM-62216, UUM-70600)
    float3 n = float3(f.x, f.y, 1.0 - (f.x < 0 ? -f.x : f.x) - (f.y < 0 ? -f.y : f.y));

    //float2 val = 1.0 - abs(n.yx);
    //n.xy = (n.zz < float2(0.0, 0.0) ? (n.xy >= 0.0 ? val : -val) : n.xy);

    // Optimized version of above code:
    float t = max(-n.z, 0.0);
    n.xy += float2(n.x >= 0.0 ? -t : t, n.y >= 0.0 ? -t : t);

    return normalize(n);
}

八面体编码后只有两个分量，Unity 将两个分量存进 RGB 3 个通道中，每个分量占 12 位。

// Pack float2 (each of 12 bit) in 888
uint3 PackFloat2To888UInt(float2 f)
{
    uint2 i = (uint2) (f * 4095.5);
    uint2 hi = i >> 8;
    uint2 lo = i & 255;
    // 8 bit in lo, 4 bit in hi
    uint3 cb = uint3(lo, hi.x | (hi.y << 4));
    return cb;
}

// Pack float2 (each of 12 bit) in 888
float3 PackFloat2To888(float2 f)
{
    return PackFloat2To888UInt(f) / 255.0;
}

// Unpack 2 float of 12bit packed into a 888
float2 Unpack888UIntToFloat2(uint3 x)
{
    // 8 bit in lo, 4 bit in hi
    uint hi = x.z >> 4;
    uint lo = x.z & 15;
    uint2 cb = x.xy | uint2(lo << 8, hi << 8);

    return cb / 4095.0;
}

// Unpack 2 float of 12bit packed into a 888
float2 Unpack888ToFloat2(float3 x)
{
    uint3 i = (uint3) (x * 255.5); // +0.5 to fix precision error on iOS
    return Unpack888UIntToFloat2(i);
}

Shadertoy 上有演示程序，右上角的数字是保存两个分量使用的总 bits 数

参考

常见的还有球坐标编码，但是涉及较多三角函数计算，性能不太好。

切线计算¶

正经项目中应该使用 MikkTSpace，这里只记录基本的数学原理。

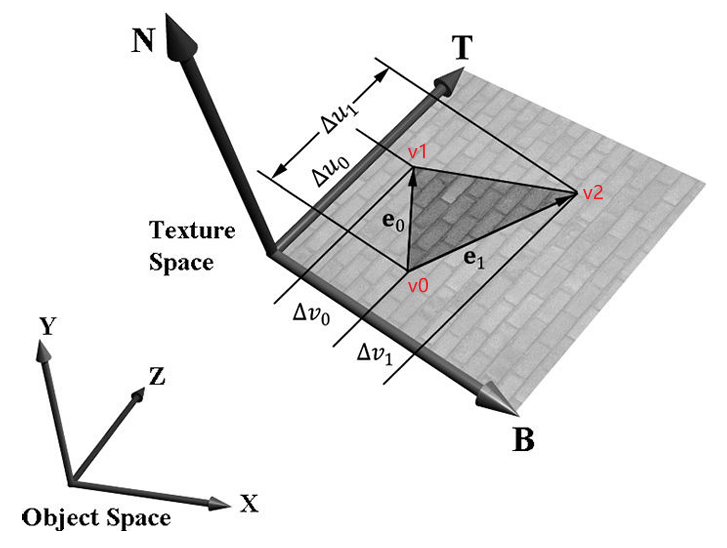
上图中，三角形的三个顶点为 \(\mathbf{v}_0,\mathbf{v}_1,\mathbf{v}_2\)。规定每个顶点的 tangent 和 u 轴方向一致，bitangent 和 v 轴方向一致，那么

\[ \begin{align} \mathbf{e}_0&=\Delta u_0 \mathbf{T} + \Delta v_0 \mathbf{B}\\ \mathbf{e}_1&=\Delta u_1 \mathbf{T} + \Delta v_1 \mathbf{B} \end{align} \]

其中

\[ \begin{align} \mathbf{e}_0&=\mathbf{v}_1-\mathbf{v}_0\\ \mathbf{e}_1&=\mathbf{v}_2-\mathbf{v}_0 \end{align} \]

所以

\[ \begin{align} \begin{bmatrix} \mathbf{T}\\ \mathbf{B} \end{bmatrix} &= \begin{bmatrix} \Delta u_0 &\Delta v_0\\ \Delta u_1 &\Delta v_1 \end{bmatrix}^{-1} \begin{bmatrix} \mathbf{v}_1-\mathbf{v}_0\\ \mathbf{v}_2-\mathbf{v}_0 \end{bmatrix}\\ \\ &= \frac{1}{\Delta u_0 \Delta v_1 - \Delta u_1 \Delta v_0} \begin{bmatrix} \Delta v_1 &-\Delta v_0\\ -\Delta u_1 &\Delta u_0 \end{bmatrix} \begin{bmatrix} \mathbf{v}_1-\mathbf{v}_0\\ \mathbf{v}_2-\mathbf{v}_0 \end{bmatrix} \end{align} \]

伪代码

for (Triangle& tri : triangles)
{
    Vertex& v0 = Vertices[tri.index0];
    Vertex& v1 = Vertices[tri.index1];
    Vertex& v2 = Vertices[tri.index2];

    float3 dp0 = v1.position - v0.position;
    float3 dp1 = v2.position - v0.position;
    float2 duv0 = v1.uv - v0.uv;
    float2 duv1 = v2.uv - v0.uv;

    float rcpDet = 1.0f / (duv0.x * duv1.y - duv1.x * duv0.y);
    float3 t = (duv1.y * dp0 - duv0.y * dp1) * rcpDet;
    float3 b = (duv0.x * dp1 - duv1.x * dp0) * rcpDet;

    v0.tangent.xyz += t;
    v1.tangent.xyz += t;
    v2.tangent.xyz += t;
    bitangents[tri.index0] += b;
    bitangents[tri.index1] += b;
    bitangents[tri.index2] += b;
}

for (int i = 0; i < vertexCount; i++)
{
    Vertex& v = Vertices[i];
    float3 n = v.normal;
    float4 t = v.tangent;
    float3 b = bitangents[i];

    // Gram-Schmidt orthogonalize
    t.xyz = normalize(t.xyz - n * dot(n, t.xyz));

    // Calculate handedness
    t.w = dot(cross(n, t.xyz), b) < 0.0f ? -1.0f : 1.0f;

    v.tangent = t;
}

一个顶点可能被多个三角形共用，要把这些三角形对应的切线都算出来，然后求平均。求平均后，法线和切线可能不正交，所以要做施密特正交化。切线的 w 分量用来记录坐标系的手性，在 shader 中用下面的公式还原 bitangent

\[ \mathbf{B}=T_w (\mathbf{N} \times \mathbf{T}) \]

如果 \(\mathbf{T},\mathbf{B},\mathbf{N}\) 都在 Object Space，可以用下面的矩阵将 Tangent Space 的点变换到 Object Space

\[ \begin{align} \mathbf{M}_{\text{object}}&=\begin{bmatrix} \mid &\mid &\mid \\ \mathbf{T} &\mathbf{B} &\mathbf{N}\\ \mid &\mid &\mid \end{bmatrix}\\ \\ \mathbf{P}_{\text{object}}&=\mathbf{M}_{\text{object}} \mathbf{P}_{\text{tangent}} \end{align} \]

\(\mathbf{M}_{\text{object}}\) 是一个正交矩阵，所以从 Object Space 到 Tangent Space 的变换矩阵为

\[ \mathbf{M}_{\text{tangent}}=\mathbf{M}_{\text{object}}^{-1}=\mathbf{M}_{\text{object}}^T \]

参考

Computing Tangent Space Basis Vectors for an Arbitrary Mesh - Eric Lengyel
textures - How to compute tangent and bitangent vectors - Game Development Stack Exchange
DirectX 12 3D 游戏开发实战

法线贴图采样¶

float3 normalTS = _BumpMap.Sample(sampler_BumpMap, input.uv).xyz * 2.0 - 1.0;
normalTS.xy *= _BumpScale;
normalTS = normalize(normalTS);
float3 N = normalize(input.normalWS);
float3 T = normalize(input.tangentWS.xyz - dot(input.tangentWS.xyz, N) * N);
float3 B = cross(N, T) * input.tangentWS.w;
float3 bumpedNomalWS = normalize(mul(normalTS, float3x3(T, B, N))); // float3x3() 是行主序矩阵

法线贴图压缩¶

双通道¶

Normal Map 保存的是 TBN 空间下的归一化法线，z 分量是大于 0 的（接近 1），所以可以只保存 x 和 y 分量。¹

z 分量用下面的公式就能算出：

\[ z = \sqrt{1 - x^2 - y^2} \]

// x、y 分别存在 r、g 通道
float3 normalTBN = float3(normalMap.rg, 0);
normalTBN.z = sqrt(1 - dot(normalTBN.xy, normalTBN.xy));

球极投影¶

双通道保存是以精度为代价的。主要是 gpu 插值的原因。

如何通过贴图的RG通道算出B通道？- 知乎 ↩