颜色基础¶

人依靠视网膜（Retina）上的感光细胞（Photoreceptor cell）来感受光的亮度与颜色，其中

视杆细胞（Rod cell）主要在弱光环境下工作，对颜色不敏感
视锥细胞（Cone cell）主要在较亮的环境下工作，对颜色较为敏感

所以，对颜色的感知主要依靠视锥细胞。

视锥细胞¶

光是电磁波，可以用功率谱 \(P(\lambda)\) 来描述其中各个波长成分的强度（功率）。一般人的视锥细胞有 L、M、S 三种，分别对长波段、中波段、短波段比较敏感。

一束光 \(P(\lambda)\) 对 L 视锥细胞的刺激为

\[ L=\int_{0}^{\infty} P(\lambda)L(\lambda)\mathrm{d}\lambda \tag{1} \]

类似地，也会对 M、S 视锥细胞产生刺激，三种刺激可以表示为一个三维向量 \((L,M,S)\)。大脑收到这三个刺激值后，会结合人当前的心理等其他信息产生颜色的感受。

格拉斯曼定律¶

格拉斯曼定律（Grassmann's laws）是一个经验规律，说明人对颜色的感知大致是线性的。比如，两束光 \(P_1(\lambda),P_2(\lambda)\) 的颜色分别为 \(C_1,C_2\)，则 \(\alpha P_1(\lambda) + \beta P_2(\lambda)\) 的颜色为 \(\alpha C_1 + \beta C_2\)。

CIE 1931 色彩空间 ¶

假设三束光 \(P_1(\lambda),P_2(\lambda),P_3(\lambda)\) 对大脑的刺激分别为 \((L_1,M_1,S_1),(L_2,M_2,S_2),(L_3,M_3,S_3)\)，如果选得好的话，它们可以作为 \((L,M,S)\) 所在空间的一组基。根据式 \((1)\) ，利用 \(P_1(\lambda),P_2(\lambda),P_3(\lambda)\) 的线性组合能得到 \((L_1,M_1,S_1),(L_2,M_2,S_2),(L_3,M_3,S_3)\) 的线性组合，进而得到任意的 \((L,M,S)\)。所以，给定三束基准光 \(P_1(\lambda),P_2(\lambda),P_3(\lambda)\) 后，对于光 \(I(\lambda)\)，求解出下式

\[ I(\lambda)=XP_1(\lambda) + YP_2(\lambda) + ZP_3(\lambda) \]

就能用 \((X,Y,Z)\) 来表示它的颜色。

CIE RGB¶

先考虑只有一种波长的光

\[ I_{\lambda}(\lambda') = A \delta(\lambda' - \lambda) \]

科学家在一块屏幕的左边照射光 \(I_{\lambda}(\lambda')\)，右边照射光 \(\bar{r} P_1(\lambda') + \bar{g} P_2(\lambda') + \bar{b} P_3(\lambda')\)，然后不断调整 \(\bar{r},\bar{g},\bar{b}\) 使得两边看上去相同。将光 \(P_1(\lambda')\) 照到左边 \(I_{\lambda}(\lambda')\) 上就能模拟 \(\bar{r} < 0\) 的情况，\(\bar{g}<0\) 和 \(\bar{b} < 0\) 同理。将可见光谱上所有的波长 \(\lambda\) 都测一遍，就得到了下图。

The normalized CIE RGB color matching functions

这是著名的颜色匹配实验。图中的三条曲线就是 CIE RGB 色彩空间的 Color matching functions，CIE 是国际照明委员会。

CIE XYZ¶

前面的图中一部分值是负数，不方便，所以又对结果做了次线性变换，换一组基准光，得到下图。

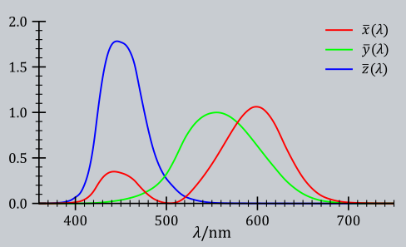
这样就得到了 CIE XYZ 色彩空间的 Color matching functions。对于任意的光 \(I(\lambda)\)，可以把它分解为不同波长光的叠加，所以

\[ \begin{align} X & = \int_0^\infty I(\lambda) \bar{x}(\lambda) \mathrm{d}\lambda\\ Y & = \int_0^\infty I(\lambda) \bar{y}(\lambda) \mathrm{d}\lambda\\ Z & = \int_0^\infty I(\lambda) \bar{z}(\lambda) \mathrm{d}\lambda\\ \end{align} \]

可以用 \((X,Y,Z)\) 来表示 \(I(\lambda)\) 的颜色。CIE XYZ 的基是精心设计的，上式中 \(Y\) 表示人感受到的颜色的亮度，但是 CIE XYZ 的基存在负功率，在物理上是不可实现的，只是一个数学模型。

CIE xyY¶

将纯光谱色（只有一种波长的光 \(I_\lambda(\lambda')\) 对应的颜色）绘制到 CIE XYZ 三维空间中，得到的是一条极其抽象的曲线。

为了方便，将它们投影到平面 \(X+Y+Z=1\) 上

\[ \begin{align} x &= \dfrac{X}{X+Y+Z}\\ y &= \dfrac{Y}{X+Y+Z}\\ z &= \dfrac{Z}{X+Y+Z} = 1-x-y \end{align} \]

若光 \(I(\lambda)\) 对应 \((X,Y,Z)\)，则光 \(A \cdot I(\lambda)\) 对应 \((AX,AY,AZ)\)，投影后都是 \((x,y,z)\)，说明投影后亮度被「归一化」了，只保留了色度（Chromaticity）。

三维平面依然不方便，注意到 \(z\) 可以用 \(x,y\) 计算出来，我们把 \(z\) 分量扔掉，将三维平面投影到 \(xOy\) 平面上，得到 CIE xy 色度图（Chromaticity diagram）。

The CIE 1931 color space chromaticity diagram

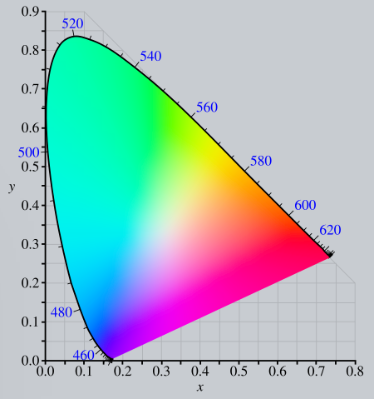
这张图的边界是纯光谱色，蓝色数字是对应的波长，内部是人眼可见的所有色度。

\(x,y\) 再加上亮度 \(Y\) 构成的空间叫 CIE xyY 空间，\(X,Z\) 可通过下式还原

\[ \begin{align} X&=\dfrac{Y}{y}x \tag{2}\\ Z&=\dfrac{Y}{y}(1-x-y) \tag{3} \end{align} \]

用于显示的 RGB 色彩空间¶

RGB 显示器的每个像素都有三个子像素，它们发出的光分别为 \(R(\lambda),G(\lambda),B(\lambda)\)，称为三原色。以它们为基可以确定一个色彩空间，对于其中颜色 \((r,g,b)\)，\(r,g,b \in [0,1]\)，像素发出的光为 \(rR(\lambda)+gG(\lambda)+bB(\lambda)\)。

色域¶

将三原色的色度标在 CIE xy 色度图上，可以围成一个三角形区域，称为色域（Gamut）。因为规定了色彩空间中 \(r,g,b \in [0,1]\)，所以只能显示出这个区域内的颜色。

白点¶

上图三角形区域中的那个点称为白点（White point），是色彩空间中 \((1,1,1)\) 对应的色度。

传递函数¶

人眼对亮度的感知不是线性的。我们相对能感知到更多暗色的变化，所以在编码和传输图像时，应该用非线性的方式，把更多空间和带宽留给暗色。

传递函数（Transfer function）	作用
OETF (opto-electronic transfer function)	将线性的颜色（光）变成非线性的图像/视频信号
EOTF (electro-optical transfer function)	将非线性的图像/视频信号变成线性的颜色（光）

sRGB¶

sRGB 是惠普和微软开发的一种标准 RGB 色彩空间，被广泛使用。上面那张色域图就是 sRGB 的色域。

参数	色度 \(x\)	色度 \(y\)
红 \(R\)	\(0.6400\)	\(0.3300\)
绿 \(G\)	\(0.3000\)	\(0.6000\)
蓝 \(B\)	\(0.1500\)	\(0.0600\)
白点 \(W\)	\(0.3127\)	\(0.3290\)

根据这些参数能算出 sRGB 的三原色在 CIE XYZ 空间的坐标。首先，白点是这个空间中最亮的颜色，它的亮度 \(Y_W\) 就规定为 \(1\)。根据式 \((2)(3)\)，红色 \(R\) 可表示为 \(\left( X_R(Y_R), Y_R, Z_R(Y_R) \right)\)，\(G,B\) 同理，由白点的定义列出方程

\[ \left\{\begin{matrix} Y_R + Y_G + Y_B = Y_W\\ X_R(Y_R) + X_G(Y_G) + X_B(Y_B) = X_W(Y_W)\\ Z_R(Y_R) + Z_G(Y_G) + Z_B(Y_B) = Z_W(Y_W) \end{matrix}\right. \]

这是关于 \(Y_R,Y_G,Y_B\) 的线性方程组，带入数据可求得

\[ \begin{bmatrix} X_R &X_G &X_B \\ Y_R &Y_G &Y_B \\ Z_R &Z_G &Z_B \end{bmatrix}=\begin{bmatrix} 0.4124 &0.3576 &0.1805 \\ 0.2126 &0.7152 &0.0722 \\ 0.0193 &0.1192 &0.9505 \end{bmatrix} \]

这个矩阵可以将 sRGB 线性空间的颜色变换到 CIE XYZ 空间

\[ \begin{bmatrix} X \\ Y \\ Z \end{bmatrix}=\begin{bmatrix} 0.4124 &0.3576 &0.1805 \\ 0.2126 &0.7152 &0.0722 \\ 0.0193 &0.1192 &0.9505 \end{bmatrix}\begin{bmatrix} R_{\text{linear}} \\ G_{\text{linear}} \\ B_{\text{linear}} \end{bmatrix} \]

CIE XYZ 的 Y 分量对应亮度，根据矩阵第二行，我们得到了 Unity Shader 里的 Luminance 函数

//
// Convert rgb to luminance with rgb in linear space with sRGB primaries and D65 white point
//
half Luminance(half3 linearRgb)
{
    return dot(linearRgb, float3(0.2126729, 0.7151522, 0.0721750));
}

sRGB 的 OETF 和 EOTF 分别为

\[ C_\text{srgb}=\begin{cases} 12.92 C_\text{linear}&, C_\text{linear} \le 0.0031308\\ 1.055 \left( C_\text{linear}^{1/2.4} \right) - 0.055&, C_\text{linear} > 0.0031308 \end{cases} \]

\[ C_{\text{linear}} = \begin{cases} \dfrac{C_\text{srgb}}{12.92}&, C_\text{srgb} \le 0.04045\\ \left (\dfrac{C_\text{srgb} + 0.055}{1.055} \right)^{2.4}&, C_\text{srgb} > 0.04045 \end{cases} \]

指数函数 \(x^{1/2.4}\) 在靠近 \(0\) 的地方斜率趋于无穷，会放大一些微弱的噪声，所以靠近 \(0\) 的地方使用线性函数代替。

近似公式为

\[ C_\text{srgb} = C_\text{linear}^{1/2.2} \]

\[ C_\text{linear} = C_\text{srgb}^{2.2} \]

Gamma

Gamma 是一个非线性变换，一般定义为

\[ V_{\text{out}} = A V_{\text{in}}^\gamma \]

通常情况下，\(A=1\) 且输入和输出都在 \([0,1]\) 范围

\(0 < \gamma < 1\) 时，称为 Gamma 压缩、Gamma 校正。
\(\gamma > 1\) 时，称为 Gamma 展开、去 Gamma 校正。

早期的阴极射线管显示器（CRT Display）输出亮度 \(I\) 与输入电压 \(u\) 的关系为

\[ I=u^{\gamma} \]

其中 \(\gamma > 1\)。所以，要对输入信号做一次 Gamma 校正

\[ u_{\text{o}} = u_{\text{i}}^{1/\gamma} \]

才能将输入正确地显示出来。sRGB 传递函数的近似公式也是这个形式，是兼容 CRT Display 的。

sRGB 应用非常广泛，所以有了一些约定俗成的说法，见下表。

简称	实际内容
线性颜色	sRGB 线性空间的颜色 \(C_{\text{linear}}\)
sRGB 颜色、非线性颜色	\(C_{\text{linear}}\) 经过 OETF 后得到的非线性颜色 \(C_{\text{srgb}}\)
线性色彩空间	sRGB 线性空间
Gamma 色彩空间	非线性颜色 \(C_{\text{srgb}}\) 所在的空间
Gamma 校正（Gamma correction）	sRGB 的 OETF
去 Gamma 校正	sRGB 的 EOTF

色温¶

在热力学中，黑体（Black body）是一个理想化的物体，它能够吸收外来的全部电磁辐射，并且不会有任何的反射与透射。随着温度上升，黑体所辐射出来的电磁波与光线则称做黑体辐射。

将上面的关系绘制在色度图上，可以得到一条曲线，被称为普朗克轨迹（Planckian locus）。

Planckian locus in the CIE 1931 chromaticity diagram

光源的色温（Color temperature）定义为与光源发出相似的光的黑体辐射体所具有的开尔文温度。在实际应用中，只有当光源发出的光和黑体辐射的光类似时，色温才有定义。

通常会用普朗克轨迹上的颜色作为白点，例如前面 sRGB 的白点 D65 就是 6500K 时的颜色。

标准光源¶

CIE 负责颁布标准光源（Standard illuminant），这个标准包含多个系列，其中 D 系列是自然日光（natural daylight）光源，例如前面的 D65 就是中午的日光（noon daylight）。

参考¶

本文的图片来自 Wikipedia 和上述文章。

HDR display in Call of Duty¶

PowerPoint presentation: HDR in Call of Duty。

相关文章
颜色准确性