渲染方程¶

Reflection at a Point¶

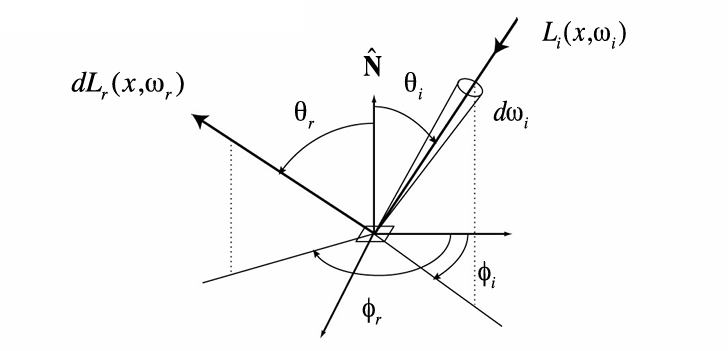
Radiance from direction \(\omega_i\) turns into the power \(E(\omega_i)\) that \(\mathrm{d}A\) receives. Then power \(E(\omega_i)\) will become the radiance to any other direction \(\omega_r\).

Differential irradiance incoming: \(\mathrm{d}E(\omega_i)=L_i(\omega_i) \cos \theta_i \mathrm{d} \omega_i\)
Differential radiance exiting due to \(\mathrm{d}E(\omega_i)\): \(\mathrm{d}L_r(\omega_r)\)

BRDF¶

The Bidirectional Reflectance Distribution Function (BRDF) represents how much light is reflected into each outgoing direction \(\omega_r\) from each incoming direction.

\[ f_r(\omega_i \rightarrow \omega_r)=\frac{\mathrm{d}L_r(\omega_r)}{\mathrm{d}E_i(\omega_i)}=\frac{\mathrm{d}L_r(\omega_r)}{L_i(\omega_i) \cos \theta_i \mathrm{d} \omega_i} \]

The unit is \(sr^{-1}\)。

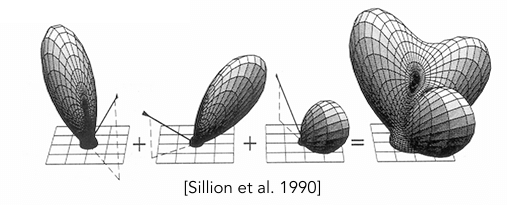
这是一个以立体角为自变量的函数，画出来通常是气球形状的，类似极坐标里的一些函数。

Properties¶

Non-negativity

\[ f_r(\omega_i \rightarrow \omega_r) \ge 0 \]
Linearity

Linearity
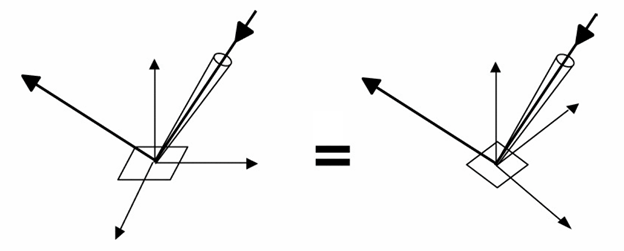
Reciprocity principle

\[ f_r(\omega_r \rightarrow \omega_i)=f_r(\omega_i \rightarrow \omega_r) \]
Energy conservation

\[ \forall \omega_r \quad \int_{H^2} f_r(\omega_i \rightarrow \omega_r) \cos \theta_i \mathrm{d} \omega_i \le 1 \]
If isotropic

\[ f_r(\omega_i \rightarrow \omega_r)=f_r(\theta_i,\phi_i;\theta_r,\phi_r)=f_r(\theta_i,\theta_r,|\phi_r-\phi_i|) \]

各向同性（Isotropic）时，比各向异性（Anisotropic）少一个维度。

Isotropic

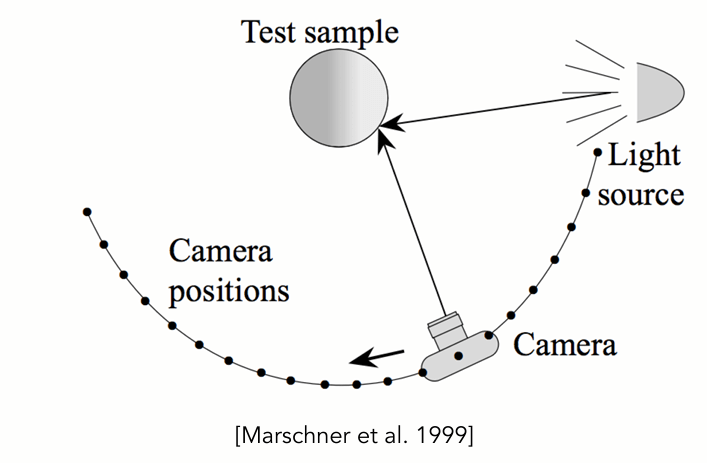
Measurement¶

foreach outgoing direction wo
    move light to illuminate surface with a thin beam from wo
    for each incoming direction wi
        move sensor to be at direction wi from surface
        measure incident radiance

Improving efficiency:

Isotropic surfaces reduce dimensionality from 4D to 3D
Reciprocity reduces the number of measurements by half
Clever optical systems...

The Reflection Equation¶

\[ L_r(p,\omega_r)=\int_{H^2} f_r(p,\omega_i \rightarrow \omega_r)L_i(p,\omega_i) \cos \theta_i \mathrm{d} \omega_i \]

The Rendering Equation¶

Kajiya 提出 The Rendering Equation，就是自发光 + 反射光。

\[ L_o(p, \omega_o) = L_e(p, \omega_o) + \int_{H^2} f_r(p,\omega_i \rightarrow \omega_o)L_i(p,\omega_i) (n \cdot \omega_i) \mathrm{d} \omega_i \]

其中 \(n \cdot \omega_i = \cos \theta_i\)。

Ray Tracing¶

渲染方程中，未知的量只有 \(L_o(p, \omega_o)\) 和 \(L_i(p,\omega_i)\)，但某一点的 \(L_i(p,\omega_i)\) 又依赖其他点的 \(L_o(p, \omega_o)\)，形成了递归。积分是线性运算，如果用某个线性算子 \(K\) 改写渲染方程，能得到

\[ L = E + KL \]

可以把 \(K\) 看作某种变换矩阵，解得

\[ L = (I-K)^{-1}E \]

对 \((I-K)^{-1}\) 用二项式定理，或者类似 \(\dfrac{1}{1-x}\) 的泰勒展开得到

\[ \begin{align} L &= (I + K + K^2 + K^3 + \cdots) E\\ &= E + KE + K^2E + K^3E + \cdots \end{align} \]

项	意义
\(E\)	Emission directly From light sources
\(KE\)	Direct illumination on surfaces
\(K^2E\)	One bounce indirect illumination, e.g., Mirrors, Refraction
\(K^3E\)	Two bounce indirect illumination
\(\cdots\)	\(\cdots\)

光栅化渲染中，前两项比较容易，后面的项就困难了。后来，提出光线追踪来解决这个问题。

后面的项计算一定数量后就差不多收敛了，再计算差别也不大了。