并查集¶

并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。它支持两种操作：

查询（find）：查询某个元素属于哪一个集合。
合并（union）：将两个集合合并为一个集合。

基本实现¶

并查集的基本思想就是以集合中的一个元素代表整个集合。

我们可以用一个树形的结构来表示一个集合，树上每一个结点都表示集合中的一个元素，树的根结点又可以用来代表整个集合。

使用一个数组 fa[] 来保存每一个结点的父结点。

int fa[MAX_N];

初始化¶

一开始，每一个元素都在不同的集合中，所以每一个结点的父结点都是它自己。

// 初始化
void init(int n)
{
    for (int i = 1; i <= n; ++i)
        fa[i] = i;
}

查询¶

查询时，只需要一层一层向上查询父结点，直到找到根结点。根结点的标志就是它的父结点依然是它本身。

递归¶

// find 操作
int find(int x)
{
    return (x == fa[x]) ? x : find(fa[x]);
}

非递归版本¶

// find 操作
int find(int x)
{
    while (x != fa[x])
        x = fa[x];
    return x;
}

如果要判断两个元素是否在同一个集合，只需要比较它们两个的根结点是否相同。

合并¶

合并时，只需要将其中一个集合的根结点的父结点设置为另一个集合的根结点。

// union 操作
void unionSet(int i, int j)
{
    fa[find(i)] = find(j);
}

路径压缩¶

很容易看出，上面合并和查找的时间复杂度都为 \(O(h)\)，\(h\) 为树的深度。

然而在某些情况下，一些集合的树可能形成一条长长的链，导致每一次查询的时间复杂度极高。考虑到我们只关心一个结点的根结点是谁，我们可以在每次 find 操作时，把路径上每一个结点的父结点直接设置为根结点，以此来减小树的深度。

递归¶

// 路径压缩 find
int find(int x)
{
    return (x == fa[x]) ? x : (fa[x] = find(fa[x]));
}

非递归版本¶

// 路径压缩 find
int find(int x)
{
    int root = x;

    // 找到根结点
    while (root != fa[root])
        root = fa[root];

    // 将路径上每一个结点的父结点设置为根结点
    while (x != root)
    {
        int temp = fa[x];
        fa[x] = root;
        x = temp;
    }

    // 返回根结点
    return root;
}

启发式合并（按秩合并）¶

在合并集合 \(A\) 和 \(B\) 时，无论将 \(A\) 合并进 \(B\) 还是将 \(B\) 合并进 \(A\)，结果都是正确的。然而不同的合并方式可能会对接下来查询的时间复杂度产生影响。如果将深度小的树合并到深度较大的树中，那么下一次查询时显然有更优的时间复杂度。

再使用一个数组 rank[] 来保存每一个结点的子树的深度（即以它为根结点的树的深度）。

int rank[MAX_N];

// 按秩合并 初始化
void init(int n)
{
    for (int i = 1; i <= n; ++i)
    {
        fa[i] = i;
        rank[i] = 1; // 一开始深度都是 1
    }
}

// 按秩合并 union 操作
void unionSet(int i, int j)
{
    // 找到两个根结点
    int x = find(i);
    int y = find(j);

    // 将深度小的树合并到深度大的树
    if (rank[x] <= rank[y])
        fa[x] = y;
    else
        fa[y] = x;

    // 如果两棵树的深度相同且根节点不同，则新树的深度 + 1
    if (rank[x] == rank[y] && x != y)
        rank[y]++;
}

需要注意的是，如果路径压缩和按秩合并一起使用，很可能会使 rank[] 的准确性降低。此时 rank[] 保存的是树深度的一个上界。

Quick Find¶

可以快速进行 find 操作，也就是可以快速判断两个节点是否连通。

需要保证同一连通分量的所有节点的 id 值相等。id 数组用来表示节点所在的连通分量

但是 union 操作代价却很高，需要将其中一个连通分量中的所有节点 id 值都修改为另一个节点的 id 值。

public class QuickFindUF extends UF {
    public QuickFindUF(int N) {
        super(N);
    }

    @Override
    public int find(int p) {
        return id[p];
    }

    @Override
    public void union(int p, int q) {
        int pID = find(p);
        int qID = find(q);

        if (pID == qID) {
            return;
        }

        for (int i = 0; i < id.length; i++) {
            if (id[i] == pID) {
                id[i] = qID;
            }
        }
    }
}

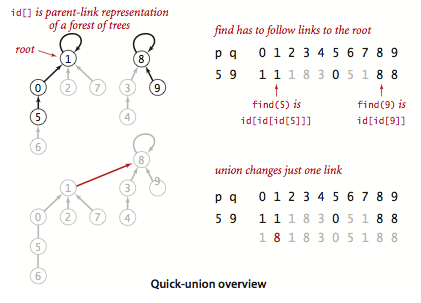
Quick Union¶

可以快速进行 union 操作，只需要修改一个节点的 id 值即可。

但是 find 操作开销很大，因为同一个连通分量的节点 id 值不同，id 值只是用来指向另一个节点。因此需要一直向上查找操作，直到找到最上层的节点。 id 数组中记录同一个分量中的另一个节点名称，根节点连接指向自己

public class QuickUnionUF extends UF {
    public QuickUnionUF(int N) {
        super(N);
    }

    @Override
    public int find(int p) {
        while (p != id[p]) {
            p = id[p];
        }
        return p;
    }

    @Override
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);

        if (pRoot != qRoot) {
            id[pRoot] = qRoot;
        }
    }
}

这种方法可以快速进行 union 操作，但是 find 操作和树高成正比，最坏的情况下树的高度为节点的数目。

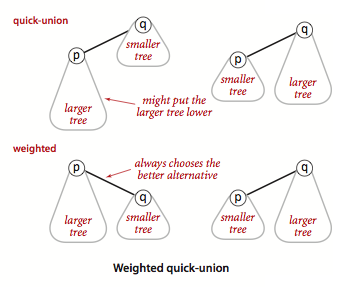
Weighted Quick Union¶

为了解决 quick-union 的树通常会很高的问题，加权 quick-union 在 union 操作时会让较小的树连接较大的树上面。

理论研究证明，加权 quick-union 算法构造的树深度最多不超过 \(\log N\)。

public class WeightedQuickUnionUF extends UF {
    private int[] sz; // 保存节点的数量信息

    public WeightedQuickUnionUF(int N) {
        super(N);
        this.sz = new int[N];
        for (int i = 0; i < N; i++) {
            this.sz[i] = 1;
        }
    }

    @Override
    public int find(int p) {
        while (p != id[p]) {
            p = id[p];
        }
        return p;
    }

    @Override
    public void union(int p, int q) {
        int i = find(p);
        int j = find(q);

        if (i == j) return;

        if (sz[i] < sz[j]) {
            id[i] = j;
            sz[j] += sz[i];
        } else {
            id[j] = i;
            sz[i] += sz[j];
        }
    }
}

路径压缩的 Weighted Quick Union¶

在检查节点的同时将它们直接链接到根节点，只需要在 find 中添加一个循环即可。

while (id[p] != p){
    id[p] = id[id[p]];
    p = id[p];
}

比较¶

算法	`union`	`find`
Quick Find	\(N\)	\(1\)
Quick Union	树高	树高
Weighted Quick Union	\(\log N\)	\(\log N\)
路径压缩的 Weighted Quick Union	非常接近 \(1\)	非常接近 \(1\)

相关文章
连通分量个数
判断图中是否有环