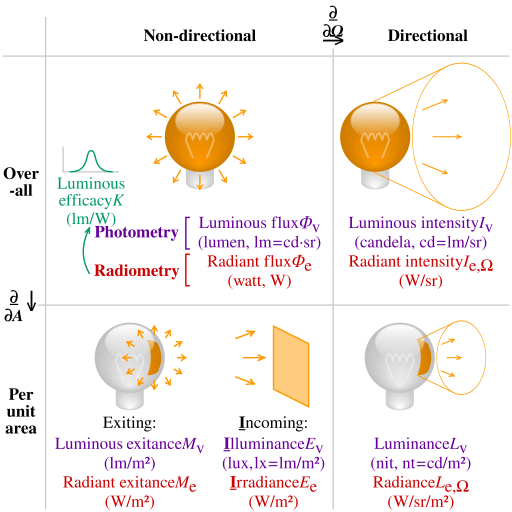
辐射度量学与光度学¶

为了物理正确地计算光照，需要了解辐射度量学（Radiometry）和光度学（Photometry）。

Comparison of photometric and radiometric quantities

Radiant energy¶

辐射能（Radiant energy）是电磁辐射的能量，用 \(Q_e\) 表示，单位是焦耳（Joule）。

Radiant / Luminous flux (power)¶

辐射通量（Radiant flux）也叫辐射功率（Radiant power），是单位时间的辐射能，单位是瓦特（Watt）。

\[ \Phi_e=\frac{\mathrm{d}Q_e}{\mathrm{d}t} \]

两种理解：

辐射源发出辐射的功率
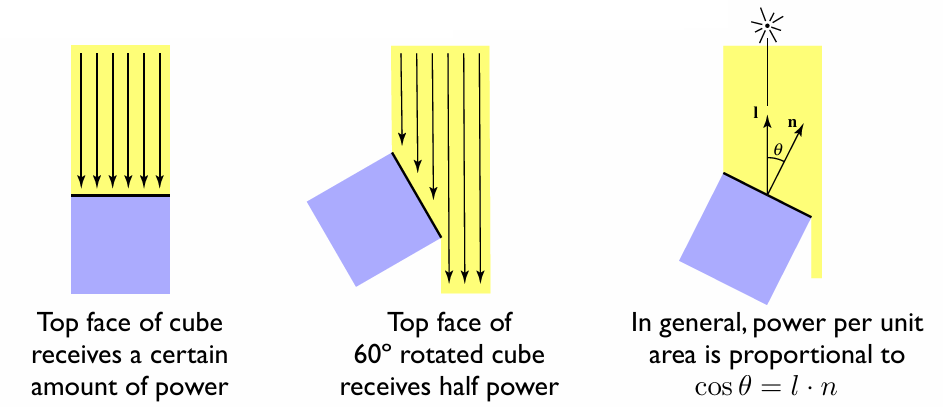
到达某一特定表面的辐射能量的功率，如果下图左边的辐射通量为 \(\Phi_1\)，那么中间 \(\Phi_2=\dfrac{\Phi_1}{2}\)，右边 \(\Phi_3 = \Phi_1 \cdot \cos \theta\)

Lambert's Cosine Law

辐射度量学研究的是所有波长的电磁辐射，其中只有一部分是人眼可见的。另一方面，在相同的辐射功率下，不同波长的光使得人眼产生的亮暗感觉不一定相同。所以，需要光度学来描述光对于人眼的强弱。

光通量（Luminous flux）就是将不同波长的辐射通量加权，折合成对人眼的有效数量，单位是 \(\text{lm}\)，即流明（Lumen）。

\[ \Phi_v= K \int_0^\infty V(\lambda) \Phi_{e,\lambda}(\lambda) \mathrm{d}\lambda \]

其中

\(K\) 表示人眼对于彩色的感知能力，是常数 \(683.002 \ \text{lm/W}\)
\(\lambda\) 是波长，单位是 \(\text{nm}\)
\(V(\lambda)\) 是光度函数 / 相对视见函数（Luminous efficiency function or Luminosity function），为人眼对不同波长光的平均视觉灵敏度（一组权重），由实验得到，没有单位
\(\Phi_{e,\lambda}(\lambda)\) 是不同波长的辐射通量密度，单位是 \(\text{W/nm}\)

Radiant / Luminous intensity¶

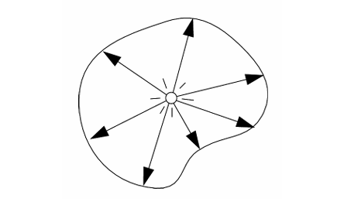
Radiant Intensity: Light Emitted From A Source

辐射强度（Radiant intensity），是给定方向上单位立体角的辐射通量，单位是 \(\text{W/sr}\)。

\[ I_e(\omega)=\frac{\mathrm{d}\Phi_e}{\mathrm{d}\omega} \]

发光强度（Luminous intensity），是给定方向上单位立体角的光通量，单位是 \(\text{lm/sr}=\text{cd}\)，即基本单位中的坎德拉（Candela）。

\[ I_v(\omega)=\frac{\mathrm{d}\Phi_v}{\mathrm{d}\omega} \]

对于各向同性点光源（Isotropic Point Source）

\[ \begin{align} \Phi &= \int_{S^2} I \mathrm{d} \omega = 4\pi I\\ \\ I &= \frac{\Phi}{4\pi} \end{align} \]

Irradiance / Illuminance¶

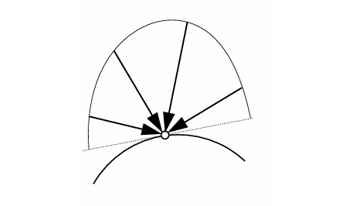
辐照度（Irradiance）是某点上单位面积的辐射通量，单位是 \(\text{W/}\text{m}^2\)。

\[ E_e(\mathbf{x})=\frac{\mathrm{d}\Phi_e(\mathbf{x})}{\mathrm{d}A} \]

照度（Illuminance）是某点上单位面积的光通量，单位是 \(\text{lx=lm/}\text{m}^2\)，即勒克斯（Lux）。

\[ E_v(\mathbf{x})=\frac{\mathrm{d}\Phi_v(\mathbf{x})}{\mathrm{d}A} \]

注意

\(\Phi_e(\mathbf{x})\) 和 \(\Phi_v(\mathbf{x})\) 是某个表面接收的通量，隐含了前面 Lambert's Cosine Law 中的 \(\cos \theta\) 项
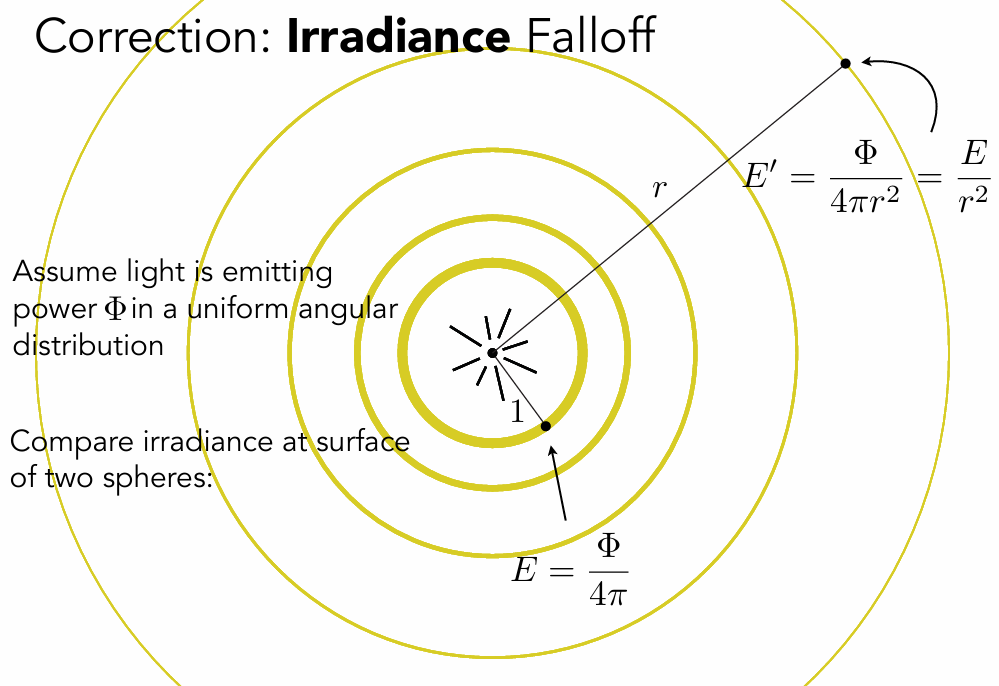
Irradiance / Illuminance 会随距离衰减，但 Radiant / Luminous Intensity 是不会衰减的

Irradiance Falloff

Radiance / Luminance¶

辐射率（Radiance）是给定方向上，单位立体角，通过单位投影面积的辐射通量，单位是 \(\text{W/}(\text{m}^2 \cdot \text{sr})\)。

\[ L_e(p,\omega)=\frac{\mathrm{d}^2 \Phi_e(p,\omega)}{\mathrm{d}\omega \mathrm{d}A \cos \theta} \]

Radiance is the fundamental field quantity that describes the distribution of light in an environment

Radiance is the quantity associated with a ray

Rendering is all about computing radiance

亮度（Luminance）是给定方向上，单位立体角，通过单位投影面积的光通量，单位是 \(\text{cd/}\text{m}^2=nt\)，即尼特（Nit）。常出现在显示器（面光源）的参数中。

\[ L_v(p,\omega)=\frac{\mathrm{d}^2 \Phi_v(p,\omega)}{\mathrm{d}\omega \mathrm{d}A \cos \theta} \]

Incident Radiance¶

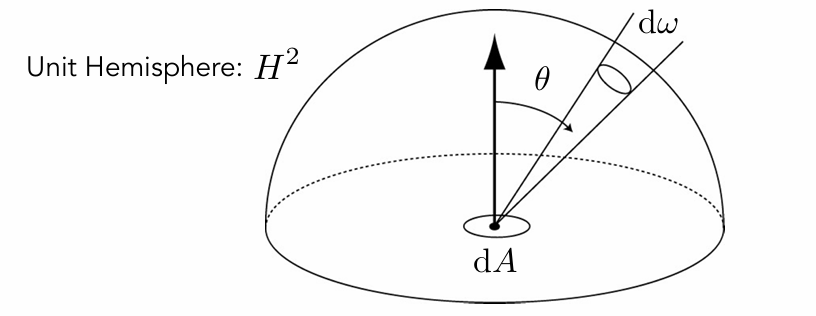
一种理解 Radiance 的方式是把 \(\mathrm{d}A\) 除上去，得到的 \(\mathrm{d} E_e(p,\omega)\) ，它是 \(p\) 处从方向 \(\omega\) 到面积 \(\mathrm{d}A\) 的 Irradiance。由于 Lambert's Cosine Law， \(\mathrm{d}E_e(p,\omega)\) 隐含了一个和物体朝向有关的 \(\cos \theta\)，但 Radiance 描述的是光线的性质，不应该和某个物体有关，所以要除以 \(\cos \theta\) ，变成单位投影面积的量。

\[ L_e(p,\omega)=\frac{\mathrm{d} E_e(p,\omega) / \cos \theta}{\mathrm{d}\omega} \]

这个公式一般用于描述 Incident Radiance: Irradiance per unit solid angle arriving at the surface. 进而计算入射的 Irradiance。

\[ \begin{align} \mathrm{d} E(p,\omega) &= L_i(p,\omega) \cos \theta \mathrm{d} \omega\\ \\ E(p) &=\int_{H^2}L_i(p,\omega) \cos \theta \mathrm{d} \omega \end{align} \]

Exiting Radiance¶

另一种理解 Radiance 的方式是把 \(\mathrm{d}\omega\) 除上去，得到 \(\mathrm{d}I_e(p,\omega)\)，然后除以 \(\mathrm{d}A\) 的投影面积。

\[ L_e(p,\omega)=\frac{\mathrm{d} I_e(p,\omega)}{\mathrm{d}A \cdot \cos \theta} \]

这个公式一般用于描述 Exiting Radiance: The intensity per unit projected area leaving the surface.