跳转至

光线与表面求交

光线追踪 涉及大量 Ray-Surface Intersection 计算。

Equations

Type Equation
Ray \(\mathbf{r}(t)=\mathbf{o}+t\mathbf{d},0 \le t < \infty\)
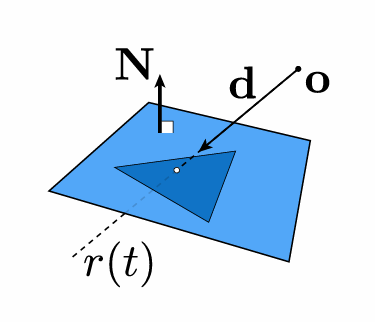
Sphere \(\mathbf{p}:(\mathbf{p}-\mathbf{c})^2-R^2=0\)
Plane \(\mathbf{p}:(\mathbf{p}-\mathbf{p}') \cdot \mathbf{N}=0\)
General implicit surface \(\mathbf{p}:f(\mathbf{p})=0\)

联立就能算出交点。

对于射线（Ray），计算后要检查参数 \(t\) 的范围。对于封闭的曲面，如果 Ray 和它交于两点且 \(t_1<0,t_2>0\)，则说明 Ray 的起点在曲面内部。

Ray Intersection With Triangle

因为 Triangle Mesh 比较常用，所以考虑 Ray 和 Triangle 的相交计算，可以分两步

  1. 计算 Ray 与 Triangle 所在 Plane 的交点
  2. 判断交点是否在 Triangle 内部，可以用 重心坐标

Ray Intersection With Triangle
Ray Intersection With Triangle

Möller Trumbore Algorithm

这个算法比前面的更快，可以一步到位。将 Ray 和三角形重心坐标式联立

\[ \mathbf{O}+t\mathbf{D}=(1-b_1-b_2)\mathbf{P_0}+b_1 \mathbf{P_1} + b_2 \mathbf{P_2} \]

其中 \(\mathbf{P_0},\mathbf{P_1},\mathbf{P_2}\) 是三角形顶点。式中的向量都是三维的，变量也只有 \(t,b_1,b_2\) 三个，所以它是一个线性方程组

\[ \begin{bmatrix} -\mathbf{D}, \mathbf{P_1}-\mathbf{P_0}, \mathbf{P_2}-\mathbf{P_0} \end{bmatrix} \begin{bmatrix} t\\ b_1\\ b_2 \end{bmatrix} = \mathbf{O}-\mathbf{P_0} \]

用 Cramer's rule 和 行列式性质（向量混合积） 求解

\[ \begin{bmatrix} t\\ b_1\\ b_2 \end{bmatrix} = \frac{1}{\mathbf{S_1} \cdot \mathbf{E_1}} \begin{bmatrix} \mathbf{S_2} \cdot \mathbf{E_2}\\ \mathbf{S_1} \cdot \mathbf{S}\\ \mathbf{S_2} \cdot \mathbf{D} \end{bmatrix} \]

其中

\[ \begin{align} \mathbf{E_1}&=\mathbf{P_1}-\mathbf{P_0}\\ \mathbf{E_2}&=\mathbf{P_2}-\mathbf{P_0}\\ \mathbf{S}&=\mathbf{O}-\mathbf{P_0}\\ \mathbf{S_1}&=\mathbf{D} \times \mathbf{E_2}\\ \mathbf{S_2}&=\mathbf{S} \times \mathbf{E_1} \end{align} \]

Cost = 1 div, 27 mul, 17 add.

Bounding Volumes

直接用 Ray 和场景中所有 Triangle 做测试太慢了，所以用简单的形状把物体包起来

  • 物体必须被完全包含在包围盒中
  • 如果 Ray 不与包围盒相交，一定也不与物体相交
  • 先检测包围盒，再检测里面的物体

Bounding Volumes
Bounding Volumes

Axis-Aligned Bounding Box

AABB 由三组轴对齐的平行面（slab）构成。轴对齐可以减少计算量。

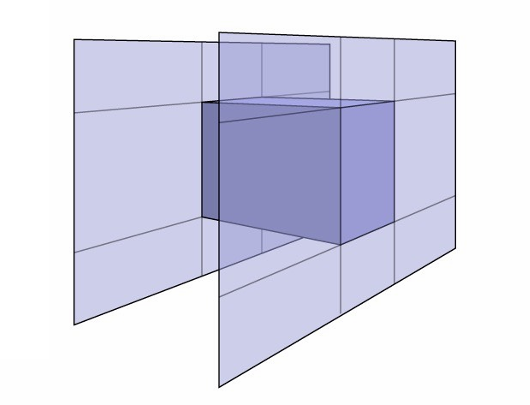
Box is the intersection of 3 pairs of slabs
Box is the intersection of 3 pairs of slabs

以 2D 为例，计算交点时，先计算 Ray 与三组平行面的交点，然后取最大的 \(t_{\text{min}}\) 和最小的 \(t_{\text{max}}\)，换句话说，就是取下图中红色部分的交集。

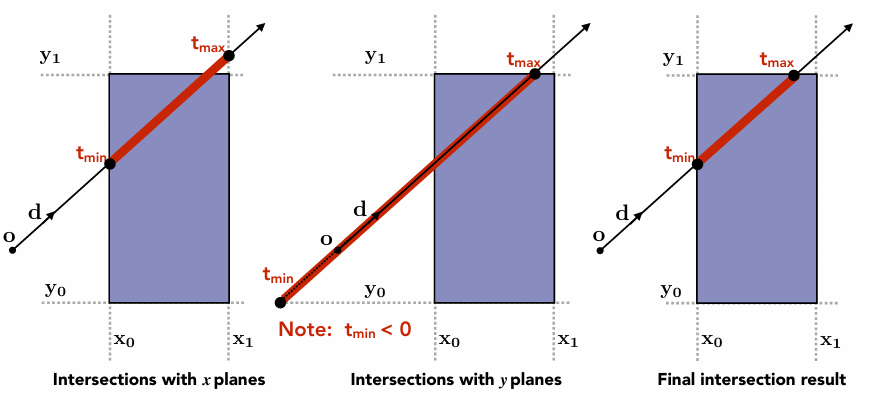
Ray Intersection with Axis-Aligned Box
Ray Intersection with Axis-Aligned Box

  • The ray enters the box only when it enters all pairs of slabs
  • The ray exits the box as long as it exits any pair of slabs

For the 3D box

\[ \begin{align} t_{\text{enter}}&=\max\{t_{\text{min}}\}\\ t_{\text{exit}}&=\min\{t_{\text{max}}\} \end{align} \]
条件 解释 相交
\(t_{\text{enter}} < t_{\text{exit}}\) Ray 在 Box 中待了一会才出去 Yes
\(t_{\text{exit}}<0\) Box 在 Ray 后面 No
\(t_{\text{exit}} \ge 0\) 且 \(t_{\text{enter}}<0\) Ray 的起始位置在 Box 内 Yes

所以，Ray 与 AABB 相交的条件是 \(t_{\text{enter}}<t_{\text{exit}}\) 且 \(t_{\text{exit}} \ge 0\)。

Acceleration

Using AABBs to accelerate ray tracing.

Uniform Spatial Partitions (Grids)

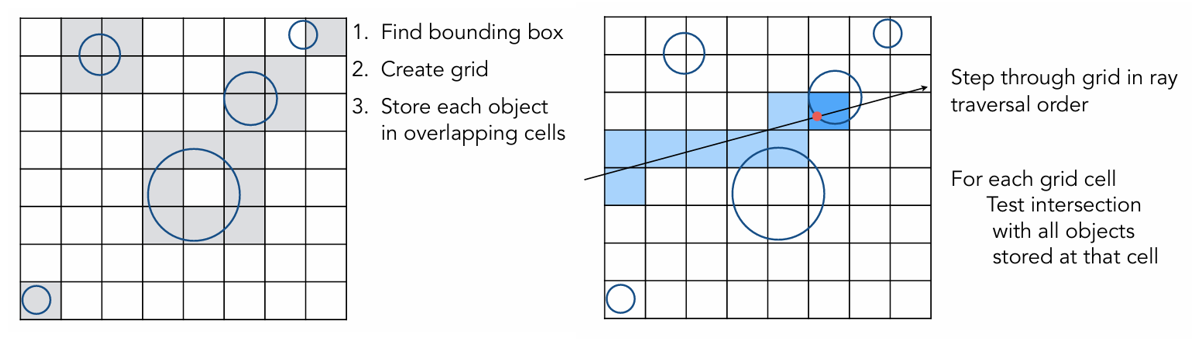
Preprocess And Ray-Scene Intersection
Preprocess And Ray-Scene Intersection

  • 划分格子数太少，没有加速效果
  • 划分格子数太多，计算量太大

一种启发式的方式

\[ \text{NumCell}=C \times \text{NumObject} \]

在 3D 场景 \(C \approx 27\)。

Plant Ecosystem, 20M triangles
Plant Ecosystem, 20M triangles

Grids work well on large collections of objects that are distributed evenly in size and space.

San Miguel Scene, 10.7M triangles
San Miguel Scene, 10.7M triangles

上图这个场景非常空，就中间有几个茶壶，大多数 Grid 都是空的，无效计算多，效果差，会出现 "Teapot in a stadium" 问题。

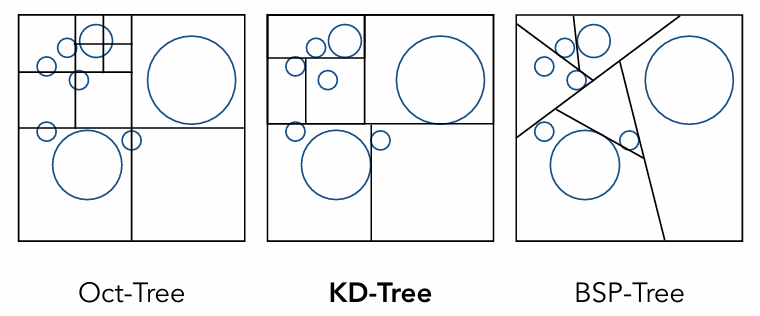
Spatial Partitions

Spatial Partitioning Examples
Spatial Partitioning Examples

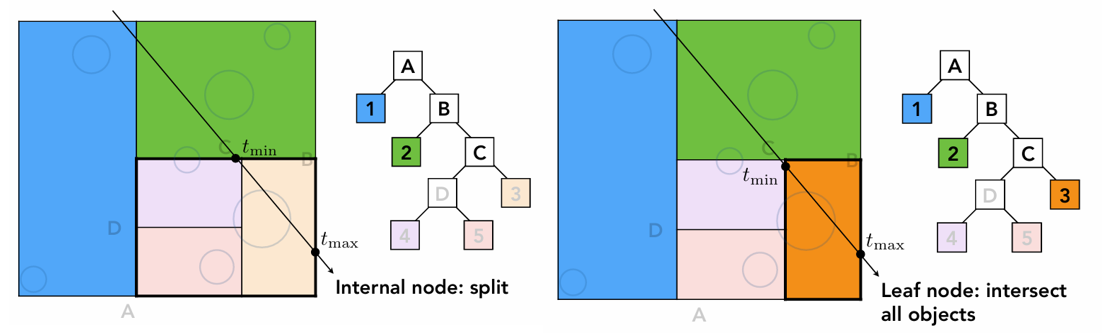
以 KD-Tree 为例，为了尽可能均匀划分，它总是 X-Y-Z 方向交替划分。下图中就是横竖交替划分。

KD-Tree Pre-Processing
KD-Tree Pre-Processing

Internal nodes store

  • split axis: x-, y-, or z-axis
  • split position: coordinate of split plane along axis
  • children: pointers to child nodes
  • No objects are stored in internal nodes

Leaf nodes store

  • list of objects

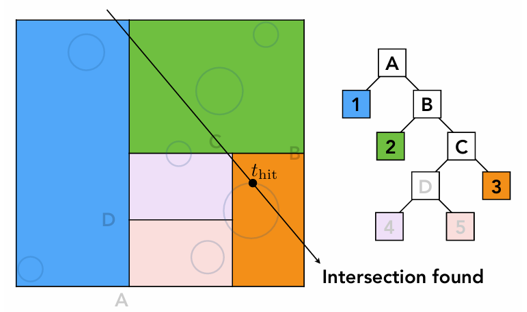
KD-Tree 遍历

Traversing a KD-Tree 1
Traversing a KD-Tree 1

Traversing a KD-Tree 2
Traversing a KD-Tree 2

Traversing a KD-Tree 3
Traversing a KD-Tree 3

Traversing a KD-Tree 4
Traversing a KD-Tree 4

Object Partitions

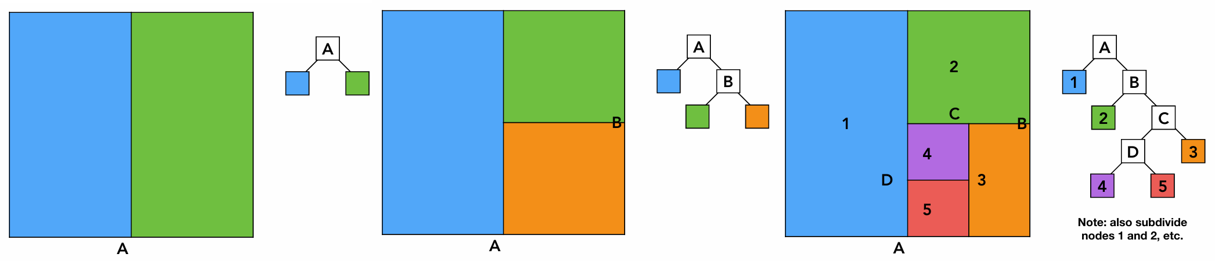
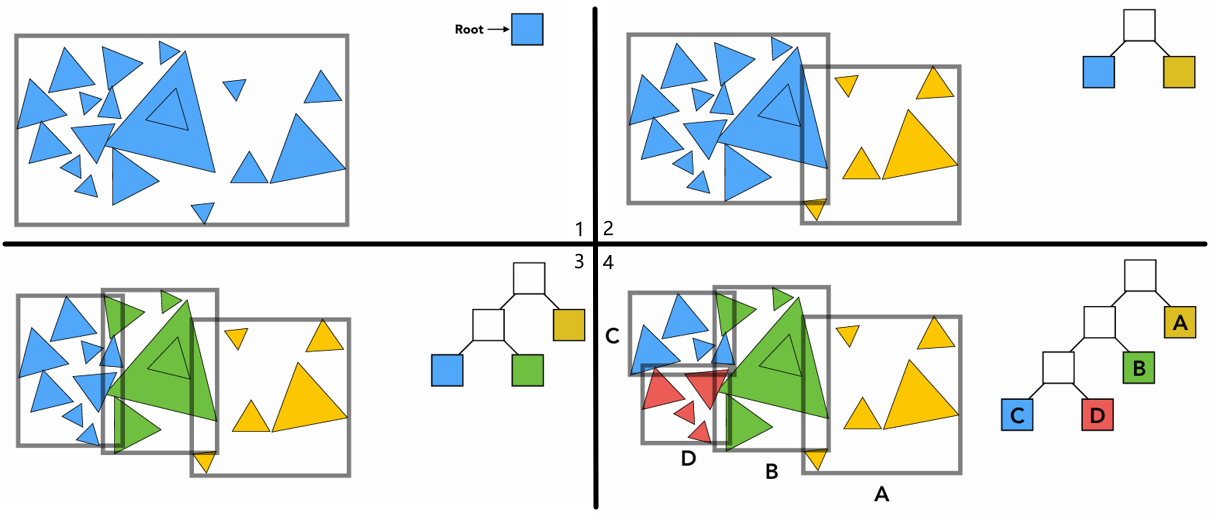
通常采用 Bounding Volume Hierarchy (BVH)。

Building BVHs
Building BVHs

BVH 构建流程

  1. Find bounding box
  2. Recursively split set of objects in two subsets
  3. Recompute the bounding box of the subsets
  4. Stop when necessary
  5. Store objects in each leaf node
  • How to subdivide a node?
    • Choose a dimension to split
    • Heuristic 1: Always choose the longest axis in node
    • Heuristic 2: Split node at location of median object
  • Termination criteria?
    • Heuristic: stop when node contains few elements
  • Internal nodes store
    • Bounding box
    • Children: pointers to child nodes
  • Leaf nodes store
    • Bounding box
    • List of objects
  • Nodes represent subset of primitives in scene
    • All objects in subtree

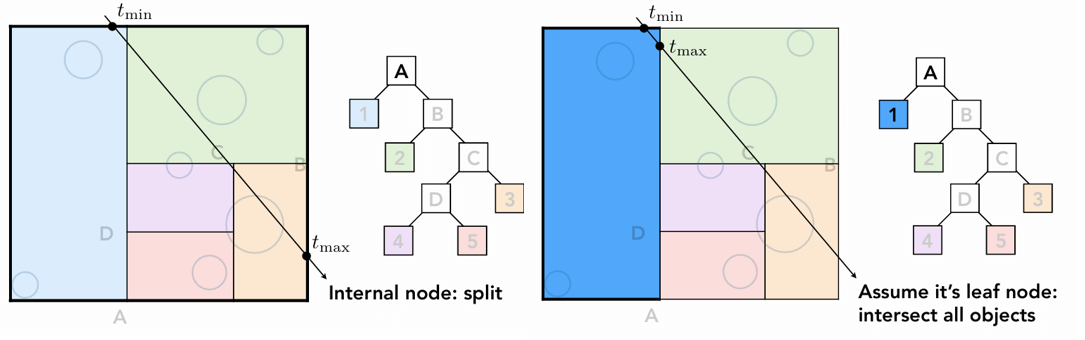
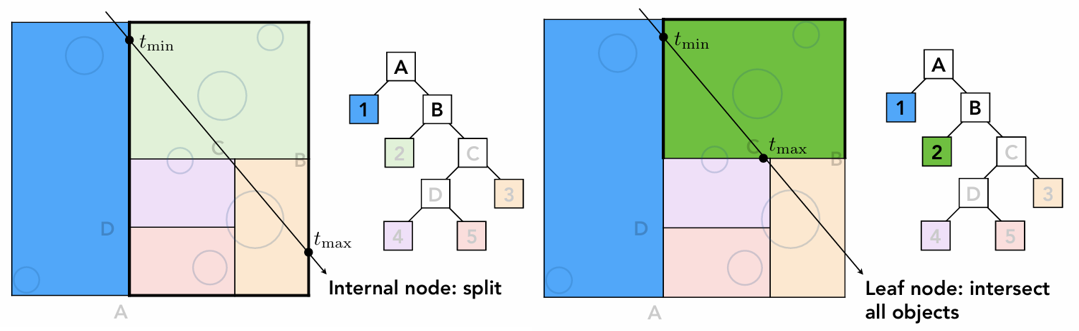
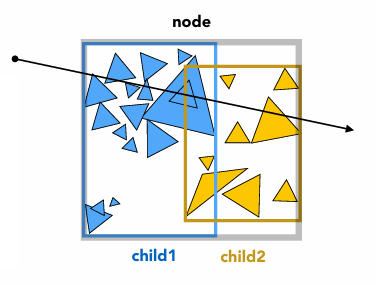
BVH 遍历

BVH Traversal
BVH Traversal

Intersect(Ray ray, BVH node)
    if (ray misses node.bbox) return;

    if (node is a leaf node)
        test intersection with all objs;
        return closest intersection;

    hit1 = Intersect(ray, node.child1);
    hit2 = Intersect(ray, node.child2);

    return the closer of hit1, hit2;

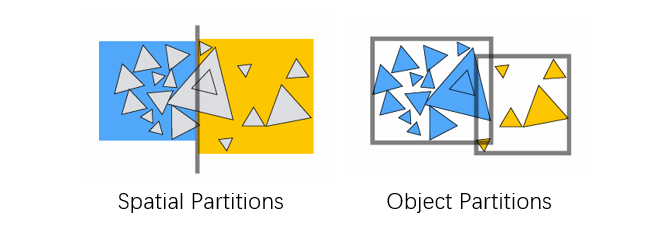
Spatial vs. Object Partitions

Spatial partition (e.g.KD-tree)

  • Partition space into non-overlapping regions
  • An object can be contained in multiple regions

Object partition (e.g. BVH)

  • Partition set of objects into disjoint subsets
  • Bounding boxes for each set may overlap in space

Spatial vs. Object Partitions
Spatial vs. Object Partitions

Spatial partition 在划分空间后，要判断哪些物体在空间中 ，而 BVH 只要重新算包围盒就好了，所以现在 BVH 使用得相对更多。

参考