体渲染¶

体渲染的建模如下

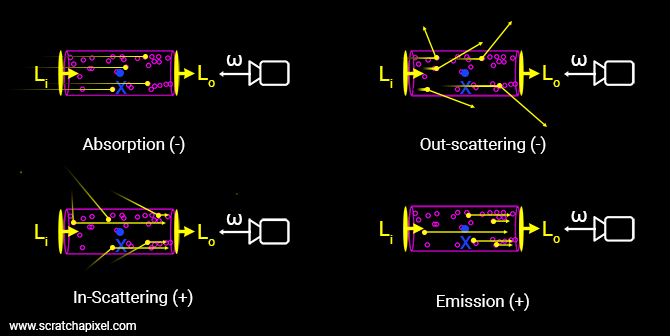
光会与其中的粒子产生作用，大致分为几种

吸收（Absorption）：入射光被粒子吸收，出射光强度变弱
外散射（Out-scattering）：入射光被粒子弹射到圆柱外面，圆柱区域的出射光强度变弱
内散射（In-scattering）：其他地方的光被粒子弹射过来，圆柱区域的出射光强度变强
放射（Emission）：粒子本身发光，使得圆柱区域的出射光强度变强

总结成公式

\[ L_o-L_i=-L_\text{absorption}-L_\text{out-scattering}+L_\text{in-scattering}+L_\text{emission} \]

Absorption Only¶

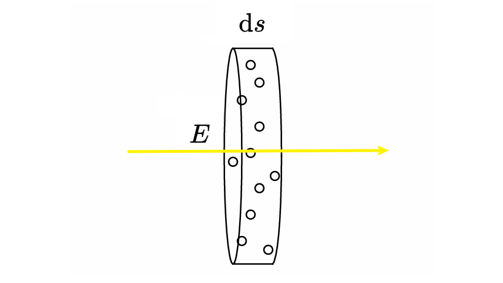
假设圆柱体的底面积为 \(E\)，粒子密度为 \(\rho\)。当圆柱体的厚度 \(\mathrm{d}s\) 足够小时，可以认为圆柱体只有一层薄薄的粒子，粒子之间不会重叠。如果粒子都是半径为 \(r\) 的球，它们占的总面积为 \(\rho \pi r^2 E\mathrm{d}s\)。

只考虑 Absorption 的话，光被吸收的概率为 \(\dfrac{\rho \pi r^2 E\mathrm{d}s}{E}=\rho \pi r^2 \mathrm{d}s\)，所以

\[ \mathrm{d}L=- \rho(s) \pi r^2 L(s)\mathrm{d}s=-\sigma(s)L(s)\mathrm{d}s \]

其中 \(\sigma(s)\) 是一个概率密度函数，\(\sigma(s)\mathrm{d}s\) 表示在 \(s\) 处光被吸收的概率。

Beer–Lambert Law¶

前面的微分方程解得

\[ L(s)=L_0 e^{-\displaystyle\int_0^s \sigma(t) \mathrm{d}t} \]

光的强度呈指数衰减，这被称为 Beer–Lambert Law。

Optical Depth¶

定义光学厚度（Optical Depth / Optical Thickness）

\[ \tau(s_1 \rightarrow s_2)=\int_{s_1}^{s_2} \sigma(t) \mathrm{d}t \]

Transmittance¶

定义透射比（Transmittance）

\[ T(s_1 \rightarrow s_2)=\frac{L(s_2)}{L(s_1)}=e^{-\displaystyle\int_{s_1}^{s_2} \sigma(t) \mathrm{d}t} = e^{-\displaystyle\tau(s_1 \rightarrow s_2)} \]

重要性质

\[ T(s_1 \rightarrow s_2)=T(s_1 \rightarrow s') \cdot T(s' \rightarrow s_2) \]

Transfer Function¶

参考前面的 Absorption，可以列出完整方程（对应一开始建模时的公式）

\[ \frac{\mathrm{d}L}{\mathrm{d}s}=-\sigma_a(s)L(s)-\sigma_s(s)L(s)+\sigma_s(s)L_s(s)+\sigma_a(s)L_e(s) \]

使用 \(\sigma_s(s)\) 和 \(\sigma_a(s)\) 区分 Scattering 和其他物理过程的概率密度
\(L_s(s)\) 是其他地方过来的 In-scattering 光，\(L_e(s)\) 是粒子的 Emission 光

通常令 \(\sigma_t=\sigma_a+\sigma_s\)，则

\[ \frac{\mathrm{d}L}{\mathrm{d}s}=-\sigma_t(s)L(s)+\sigma_s(s)L_s(s)+\sigma_a(s)L_e(s) \]

这就是传输方程（Transfer Function），右边负的那项称为衰减项，正的两项统称为源项。

Volume Rendering Equation¶

Transfer Function 是一个变系数非齐次线性微分方程，用常数变易法解得

\[ L(s)=\int_0^s e^{-\displaystyle\int_v^s\sigma_t(u)\mathrm{d}u} \bigg (\sigma_s(v)L_s(v)+\sigma_a(v)L_e(v) \bigg) \mathrm{d}v + L_0 e^{-\displaystyle\int_0^s \sigma_t(u)\mathrm{d}u} \]

In-scattering¶

参考 BRDF，前面公式中的 \(L_s\) 可以用 \(p(s, \omega_i \rightarrow \omega)\) 描述，这是一个 Phase Function，表示在 \(s\) 处 \(\omega_i\) 方向的光被散射到 \(\omega\) 方向的概率密度，用到了微分立体角，对整个球积分是 \(1\)。

\[ L_s(s,\omega)=\int_{S^2} L_i(s,\omega_i) p(s, \omega_i \rightarrow \omega) \mathrm{d}\omega_i \]

带回原方程，发现体渲染方程也和渲染方程一样变成递归方程了，而且方程里的参数也要改成各向异性的，太复杂了。

参考¶

相关文章
NeRF