NeRF
Neural Radiance Fields（NeRF）使用多层感知器（Multilayer Perceptron / MLP）隐式地学习一个 3D 场景。
Scene Representation
NeRF 使用简化的 体渲染方程 隐式表达 3D 场景。在完整方程的基础上，令 \(L_s=L_e=C\)，并忽略 \(L_0\) 可以得到
\[ \begin{align} L(s)&=\int_0^s T(v) \sigma_t(v) C(v) \mathrm{d}v\\ \\ T(v)&=e^{-\displaystyle\int_v^s \sigma_t(u)\mathrm{d}u} \end{align} \]
这样就和 NeRF 论文里的方程差不多了，但 NeRF 中使用的是 Camera Ray，积分方向是从相机到光源，和我们的积分方向相反。对我们的公式换元后，就能得到 NeRF 的公式。
\[ \begin{align} \mathbf{r}(t)&=\mathbf{o}+t\mathbf{d}\\ \\ C(\mathbf{r})&=\int_{t_n}^{t_f} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) \mathrm{d}t\\ \\ T(t)&=e^{-\displaystyle\int_{t_n}^{t} \sigma(\mathbf{r}(s)) \mathrm{d}s} \end{align} \]
其中 \(\mathbf{r}(t)\) 表示 Camera Ray 上一点，\(\mathbf{d}\) 表示方向。颜色 \(\mathbf{c}\) 与位置和视角都有关（View-Dependent），体密度 \(\sigma\) 只和位置有关。
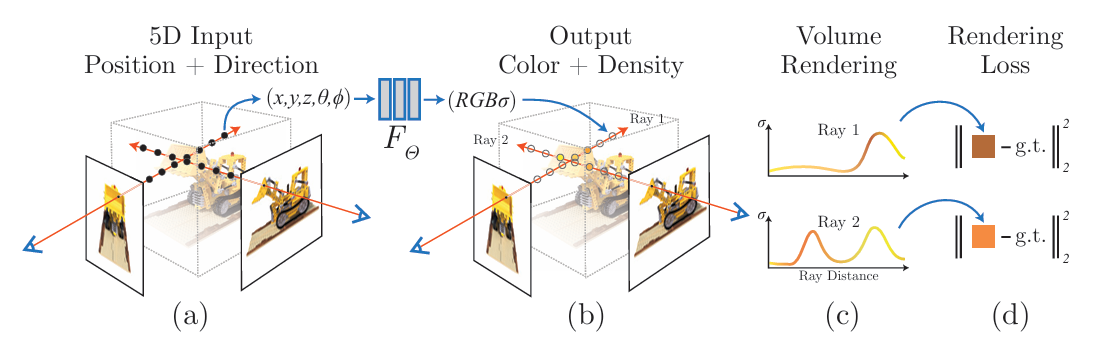NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
NeRF 实质上是给神经网络一个 5D 输入 \((\mathbf{r},\mathbf{d})=(x,y,z,\theta,\phi)\)，然后预测对应的颜色和体密度 \((\mathbf{c},\sigma)=(R,G,B,\sigma)\)，再带入体渲染方程得到该视角的画面。
Numerical Estimation of Volume Rendering
将积分区间均匀划分成 \(N\) 份
\[ C(\mathbf{r})=\sum_{i=1}^N\int_{t_n +(i-1)\Delta t}^{t_n + i\Delta t} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) \mathrm{d}t \]
其中 \(\Delta t=\dfrac{t_f-t_n}{N}\)。然后，在每段均匀采样一个点
\[ t_i \sim U \left[ t_n+(i-1) \Delta t, t_n+i \Delta t \right] \]
使用该点的 \(\mathbf{c}_i,\sigma_i\) 作为区间内的近似值，即在区间里它们是常数
\[ \begin{align} C(\mathbf{r})&\approx \sum_{i=1}^N \sigma_i \mathbf{c}_i(\mathbf{d}) \int_{t_n +(i-1)\Delta t}^{t_n + i\Delta t} T(t) \mathrm{d}t\\ \\ &\approx \sum_{i=1}^N \sigma_i \mathbf{c}_i(\mathbf{d}) \int_{t_n +(i-1)\Delta t}^{t_n + i\Delta t} \exp \left( -\displaystyle\int_{t_n}^{t} \sigma(\mathbf{r}(s)) \mathrm{d}s \right) \mathrm{d}t\\ \\ &\approx \sum_{i=1}^N \sigma_i \mathbf{c}_i(\mathbf{d}) \int_{t_n +(i-1)\Delta t}^{t_n + i\Delta t} \exp \left( -\displaystyle\int_{t_n+(i-1) \Delta t}^{t} \sigma_i \mathrm{d}s -\displaystyle\int_{t_n}^{t_n+(i-1) \Delta t} \sigma(\mathbf{r}(s)) \mathrm{d}s \right) \mathrm{d}t\\ \\ &\approx \sum_{i=1}^N \sigma_i \mathbf{c}_i(\mathbf{d}) \int_{t_n +(i-1)\Delta t}^{t_n + i\Delta t} \exp \left( \displaystyle{-\left(t-t_n-(i-1)\Delta t \right) \sigma_i -\sum_{j=1}^{i-1} \sigma_j \Delta t} \right) \mathrm{d}t\\ \\ &\approx \sum_{i=1}^N \sigma_i \mathbf{c}_i(\mathbf{d}) \exp \left(-\displaystyle\sum_{j=1}^{i-1} \sigma_j \Delta t \right) \int_{t_n +(i-1)\Delta t}^{t_n + i\Delta t} \exp \bigg(-\left(t-t_n-(i-1)\Delta t \right) \sigma_i \bigg) \mathrm{d}t\\ \\ &\approx \sum_{i=1}^N \sigma_i \mathbf{c}_i(\mathbf{d}) \exp \left(-\displaystyle\sum_{j=1}^{i-1} \sigma_j \Delta t \right) \cdot \dfrac{1}{\sigma_i} \left( 1-e^{-\sigma_i \Delta t} \right)\\ \\ &\approx \sum_{i=1}^N \exp \left(-\displaystyle\sum_{j=1}^{i-1} \sigma_j \Delta t \right) \left( 1-e^{-\sigma_i \Delta t} \right) \mathbf{c}_i(\mathbf{d})\\ \\ &\approx \sum_{i=1}^N T_i \bigg( 1-e^{-\sigma_i \delta_i} \bigg) \mathbf{c}_i \ , \quad \text{where} \ T_i = \exp \left(-\displaystyle\sum_{j=1}^{i-1} \sigma_j \delta_j \right) \end{align} \]
推导过程中 \(\delta_i=t_{i+1}-t_i=\Delta t\)，这样就得到 NeRF 论文里的离散方程了。
Positional Encoding
神经网络倾向于学习低频信息，对高频信息表现较差。
\[ \gamma(p)=\bigg( \sin (2^0 \pi p), \cos (2^0 \pi p), \cdots, \sin (2^{L-1} \pi p), \cos (2^{L-1} \pi p) \bigg) \]
NeRF 对 5D 输入的每个分量应用 \(\gamma(\cdot)\) 函数，将输入映射到更高维。对坐标 \(\gamma(\mathbf{r})\) 取 \(L=10\)，对方向 \(\gamma(\mathbf{d})\) 取 \(L=4\)，总的输入维度变成 \((3 \cdot 10 + 2 \cdot 4) \cdot 2 = 76\)。
Positional Encoding
可以借助方波的傅里叶级数来理解。MLP 在拟合时类似傅里叶级数，绝大多数地方拟合得较好，但高频的部分拟合得较差。原本的 5D 输入将 5 维空间挤得比较满，相当于输入在下图的 \(x\) 轴挤得比较满，很容易碰到高频的部分，效果就比较差。提高维度后，输入分散得比较开，不容易碰到高频部分，效果就好一点。
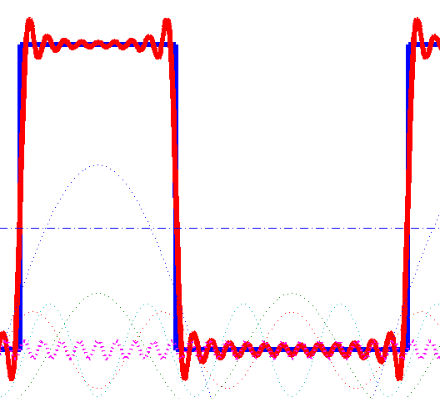The Square Wave
Hierarchical Sampling
在场景中，无用的空气区域可能占大多数，均匀采样效率较低。将前面的离散方程表示为加权求和的形式
\[ \begin{align} C &= \sum_{i=1}^N T_i \bigg( 1-e^{-\sigma_i \delta_i} \bigg) \mathbf{c}_i\\ \\ &= \sum_{i=1}^N \omega_i \mathbf{c}_i \end{align} \]
NeRF 使用了 coarse to fine 的做法，先用一个均匀采样的 coarse 网络计算 \(\omega_i\)，然后归一化出 \(\hat{\omega}_i\)
\[ \hat{\omega}_i = \frac{\omega_i}{\displaystyle\sum_{j=1}^N \omega_j} \]
它可以作为一个分段的概率密度函数，估计有效体素的分布，然后进行重要性采样。
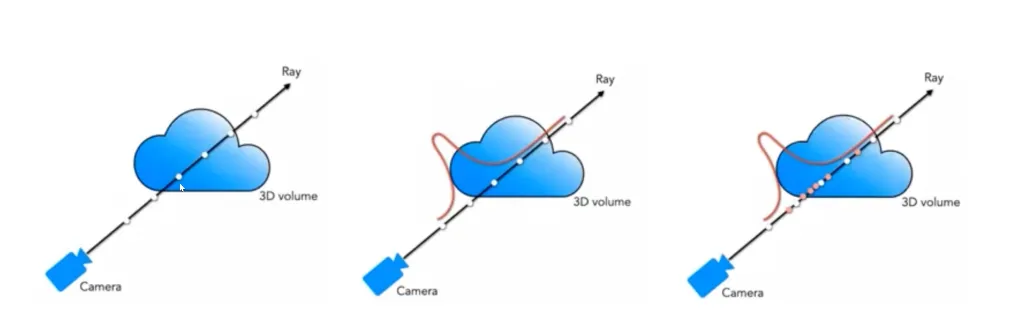Hierarchical Sampling
最后，将均匀采样值和重要性采样值都交给另一个 fine 网络，预测最终结果。
参考