蒙特卡罗方法
蒙特卡罗方法（Monte Carlo method）是指使用随机数来解决很多计算问题的方法。
积分
将积分转化为 数学期望，然后用 大数定律 近似计算
\[ \begin{align} \int_a^b f(x) \mathrm{d}x &= \int_a^b \frac{f(x)}{pdf(x)} \cdot pdf(x)\mathrm{d}x\\ \\ &=E \left ( \frac{f(X)}{pdf(X)} \right) \end{align} \]
其中 \(X \sim pdf(x)\)。按 \(X_i \sim pdf(x)\) 随机采样 \(N\) 次，然后取平均值就能估算积分结果
\[ \int_a^b f(x) \mathrm{d}x \approx \frac{1}{N} \sum_{i=1}^N \frac{f(X_i)}{pdf(X_i)} \]
如果是 均匀采样，那么 \(pdf(x)=\dfrac{1}{b-a}\)，上式变成
\[ \int_a^b f(x) \mathrm{d}x \approx \frac{b-a}{N} \sum_{i=1}^N f(X_i) \]
重要性采样
重要性采样（Importance Sampling）是一种估计期望的方法。如果 \(X \sim p(x)\)，需要随机采样 \(N\) 个 \(X_i \sim p(x)\) 来估计 \(E(f(X))\)
\[ E(f(X)) \approx \frac{1}{N}\sum_{i=1}^N f(X_i) \]
但是 \(p(x)\) 分布可能不好采样，或者方差比较大导致上式收敛太慢，这时就要换一个更好的分布 \(q(x)\)。考虑到
\[ I=E(f(X))=\int_a^b f(x)p(x) \mathrm{d}x=\int_a^b \frac{p(x)}{q(x)} f(x) q(x) \mathrm{d}x \]
所以，可以随机采样 \(N\) 个 \(X_i \sim q(x)\)，用下式来估计 \(E(f(X))\)
\[ \hat{I}_N = \frac{1}{N} \sum_{i=1}^N \frac{p(X_i)}{q(X_i)} f(X_i) \]
这显然是一个 无偏 的估计。其中，\(\dfrac{p(X_i)}{q(X_i)}\) 是重要性权重。
减少方差
\(\hat{I}_N\) 的方差为
\[ \begin{align} D \left(\hat{I}_N \right)&=\frac{1}{N^2} \sum_{i=1}^N D \left( \frac{p(X_i)}{q(X_i)} f(X_i) \right)\\ \\ &=\frac{1}{N^2} \sum_{i=1}^N \left( E \left( \frac{p^2(X_i)}{q^2(X_i)} f^2(X_i) \right) - E^2 \left( \frac{p(X_i)}{q(X_i)} f(X_i) \right) \right)\\ \\ &=\frac{1}{N} \left( \int_a^b\frac{p^2(x)f^2(x)}{q(x)}\mathrm{d}x - I^2 \right) \end{align} \]
根据柯西 - 施瓦茨不等式（Cauchy–Schwarz inequality）
\[ \int A^2(x) \mathrm{d}x \int B^2 \mathrm{d}x \ge \left( \int A(x)B(x) \mathrm{d}x \right)^2 \]
当且仅当 \(A(x)=\lambda B(x)\) 时，等号成立。把 \(A(x)\) 和 \(B(x)\) 当成向量会比较容易理解，当且仅当两个向量平行时，等号成立。
\[ \begin{align} D \left(\hat{I}_N \right)&=\frac{1}{N} \left( \int_a^b\frac{p^2(x)f^2(x)}{q(x)}\mathrm{d}x - I^2 \right)\\ \\ &=\frac{1}{N} \left( \int_a^b\frac{p^2(x)f^2(x)}{q(x)}\mathrm{d}x \underbrace{\int_a^b q(x) \mathrm{d}x}_{1} - I^2 \right)\\ \\ &\ge \frac{1}{N} \left( \left( \int_a^b f(x) p(x) \mathrm{d}x \right)^2-I^2 \right)\\ \\ &=\frac{1}{N} (I^2-I^2) = 0 \end{align} \]
当前仅当 \(q(x)=\lambda f(x)p(x)\) 时，等号成立。因为 \(q(x)\) 是概率密度函数，要满足归一化条件，所以
\[ q(x)=\frac{f(x)p(x)}{\int_a^b f(x)p(x) \mathrm{d}x} \]
这时，\(\hat{I}_N\) 的方差为 \(0\)，只要采样一次就能得到正确结果。但按照这个分布采样其实比较困难，毕竟它的分母就是我们要求的 \(I\)，要是能直接求出来就没前面那么多事了。实际应用中，应该找和最优分布接近的已知分布来采样，也能减少方差。
估计积分
前面提到，积分可以转化为期望
\[ \int_a^b f(x) \mathrm{d}x =E \left ( \frac{f(X)}{p(X)} \right), \quad X \sim p(x) \]
最简单的方法是按前面说的，均匀采样来估计结果，此时
\[ p(x)=\frac{1}{b-a} \]
我们希望找到一个更好的分布 \(q(x)\) 来减少方差，带入刚才的结论
\[ q(x)=\frac{f(x)}{\int_a^b f(x) \mathrm{d}x} \]
所以，在用蒙特卡罗方法估计积分时，应该尽量按照与 \(f(x)\) 形状相近的分布来采样，能减少方差，减少采样次数。
多重重要性采样
在估计积分时，对于更复杂的被积函数 \(f(x)\)，我们可能无法给出一个与它形状相近的 PDF 用于采样。
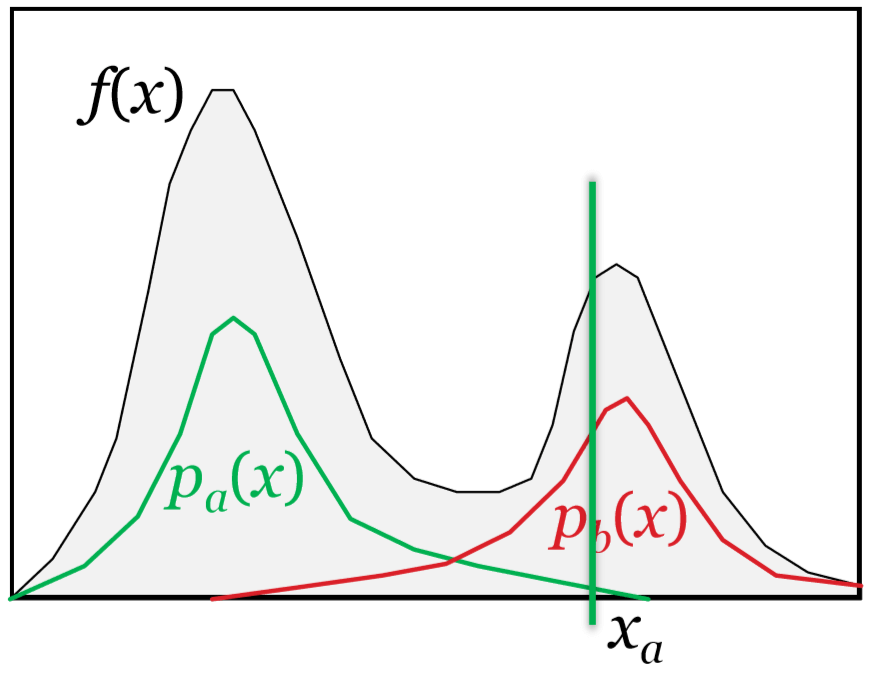更复杂的函数
假设上图中
\[ f(x)=f_a(x)f_b(x) \]
其中，\(f_a(x)\) 和 \(f_b(x)\) 是两个相对简单的函数，我们能给出与它们形状分别相近的 \(p_a(x)\) 和 \(p_b(x)\) 分布。然而，单独使用某个分布去采样，可能导致极大的方差，例如图中 \(\dfrac{f(x_a)}{p_a(x_a)}\) 是一个非常大的数，和期望差得很远。
多重重要性采样（Multiple Importance Sampling）就是结合多种分布去采样，再加权平均，进而减少方差
\[ \hat{I}_{\text{MIS}}=\sum_{i=1}^n \frac{1}{n_i} \sum_{j=1}^{n_i} \omega_i(X_{i,j}) \frac{f(X_{i,j})}{p_i(X_{i,j})} \]
其中，\(p_i\) 是用于采样的多种分布，\(X_{i,j} \sim p_i(x)\)，\(\omega_i\) 是权重函数。为了保证无偏性，要求同时满足
- 当 \(f(x) \ne 0\) 时，\(\displaystyle\sum_{i=1}^n \omega_i(x)=1\)
- 当 \(p_i(x)=0\) 时，\(\omega_i(x)=0\)
此时，可以验证一下 MIS 的期望
\[ \begin{align} E \left(\hat{I}_{\text{MIS}} \right)&=\sum_{i=1}^n \frac{1}{n_i} \sum_{j=1}^{n_i} \int_a^b \frac{\omega_i(x)f(x)}{p_i(x)} p_i(x) \mathrm{d}x\\ \\ &=\int_a^b \sum_{i=1}^n \omega_i(x)f(x) \mathrm{d}x\\ \\ &=\int_a^b f(x) \mathrm{d}x \end{align} \]
常数权重
如果 \(\omega_i(x)\) 是一个常数，那么
\[ D \left( \hat{I}_{\text{MIS}} \right)=\sum_{i=1}^n \frac{w_i^2}{n_i} D \left( \frac{f(X)}{p_i(X)} \right) \]
只要其中一个分布 \(p_i(x)\) 导致方差较大，整体的方差就会比较大。这不是一个好的策略。
The balance heuristic
The balance heuristic 策略使用
\[ \hat{\omega}_i(x)=\frac{n_i p_i(x)}{\sum_k n_k p_k(x)} \]
作为权重函数。将它带入到 MIS 估计公式中
\[ \begin{align} \hat{I}_{\text{MIS}}&=\sum_{i=1}^n \frac{1}{n_i} \sum_{j=1}^{n_i} \left( \frac{n_i p_i(X_{i,j})}{\sum_k n_k p_k(X_{i,j})} \right) \frac{f(X_{i,j})}{p_i(X_{i,j})}\\ \\ &=\sum_{i=1}^n \sum_{j=1}^{n_i} \frac{f(X_{i,j})}{\sum_k n_k p_k(X_{i,j})}\\ \\ &=\frac{1}{N} \sum_{i=1}^n \sum_{j=1}^{n_i} \frac{f(X_{i,j})}{\sum_k c_k p_k(X_{i,j})} \end{align} \]
其中，\(N=\sum_i n_i\) 是总的采样次数，\(c_k=n_k/N\) 是使用 \(p_k(x)\) 分布采样的数量占比。
The balance heuristic 策略可以较好地减小方差，可以证明，即使存在更好的权重函数 \(\omega_i(x)\)，方差也不会比 The balance heuristic 策略小很多。
The power heuristic
The power heuristic 策略使用
\[ \hat{\omega}_i(x)=\frac{(n_i p_i(x))^\beta}{\sum_k (n_k p_k(x))^\beta} \]
作为权重函数，当 \(\beta=1\) 时就是 The balance heuristic。除了 \(1\) 以外，我们通常会令 \(\beta=2\)，将它带入到 MIS 估计公式中
\[ \hat{I}_{\text{MIS}}=\frac{1}{N} \sum_{i=1}^n \sum_{j=1}^{n_i} \frac{c_i p_i(X_{i,j}) f(X_{i,j})}{\sum_k (c_k p_k(X_{i,j}))^2} \]
其中，\(X_{i,j} \sim p_i(x)\)，如果本次采样时 \(p_i(X_{i,j})\) 比较小，对结果的贡献也会比较小。The balance heuristic 策略每次采样的贡献与本次采样的分布 \(p_i(X_{i,j})\) 无关，所以叫 balance。
在实际应用中，The power heuristic 策略通常能比 The balance heuristic 策略减小更多方差。
应用
https://blog.yiningkarlli.com/2015/02/multiple-importance-sampling.html
如图，场景中有四个球形光源。场景中的五个金属条由上到下粗糙度依次增加。在这个场景下，用任何采样方式结果都收敛得都很慢。
对 BRDF 重要性采样，64 SPP
只有 BRDF lobe 范围内的光源才有贡献。如果只对 BRDF 重要性采样，对于上面低粗糙度的金属条，BRDF lobe 小，容易采样到有效的光源，方差就小，噪点少。对于下面较粗糙的金属条，BRDF lobe 大，采样范围很大，很难恰好采样到有效的光源上，方差就大，噪点多。
对光源重要性采样，64 SPP
如果只对光源重要性采样，对于下面粗糙的金属条，BRDF lobe 大，大多数光源都在 lobe 范围内，方差小，噪点少。对于上面低粗糙度的金属条，BRDF lobe 小，大部分光源都不在 lobe 范围内，无效采样多，方差大，噪点多。
多重重要性采样（BRDF + 光源），64 SPP
使用 MIS 后，效果就改善了很多。
低差异序列
使用伪随机算法生成的随机序列比较杂乱，采样点可能挤在一起。低差异序列（Low-discrepancy Sequence）则可以产生分布更加均匀的序列。
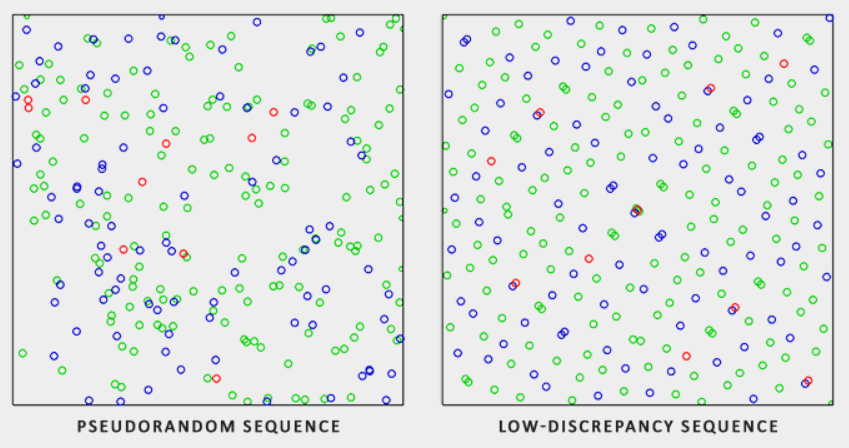伪随机序列 vs. 低差异序列
使用低差异序列采样，可以加快蒙特卡罗方法的收敛速度，这被称为拟蒙特卡罗方法（Quasi-Monte Carlo method）。
Radical Inverse
Van der Corput
Halton
Hammersley
Scrambled Halton
Sobol
参考
相关文章