跳转至

视觉期末整理

色彩

采样定理

若采样率 \(\ge\) 信号最大频率的 2 倍，或每周期两个样本，信号才能复原，该最小采样率称为奈奎斯特频率。

若采样率不够高，信号会发生混叠。

插值

  • 最近邻插值：Point
  • 双线性插值：Bilinear
  • 双三次插值：Bicubic，使用一个三次多项式 \(S(x)\) 加权周围 16 个灰度值得到
  • 前向映射：原图像的点变换到新图像，然后按权重分配给周围像素
  • 后向映射：新图像的点变换回原图像，然后插值周围的点

图像和滤波

  • 图像基本运算
    • 点运算：对一幅图像中每个像素点的灰度值进行计算的方法
      • 灰度变换增强：线性、分段线性、非线性灰度变换
      • 直方图增强
    • 几何运算：对图像做几何变换

  • 线性滤波：用相邻像素的线性组合（加权和）代替原像素

    • 互相关（Cross Correlation）：

      \[ G(i,j)=H \otimes F = \displaystyle\sum_{u=-k}^{k}\displaystyle\sum_{v=-k}^{k} H(u,v)F(i+u,j+v) \]

    • 卷积（Convolution）：

      \[ G(i,j)=H * F = \displaystyle\sum_{u=-k}^{k}\displaystyle\sum_{v=-k}^{k} H(u,v)F(i-u,j-v) \]

  • 核的大小为 \((2k+1) \times (2k+1)\)，将相关权重核旋转 180 度（水平、垂直翻转）得到卷积核

高斯滤波

利用高斯滤波函数对图像进行卷积，其中高斯函数为

\[ G_\sigma = \frac{1}{2 \pi \sigma^2} e^{-\dfrac{x^2+y^2}{2 \sigma^2}} \]

利用高斯滤波函数对图像进行多次滤波，可获得多尺度滤波图像。

高斯多尺度滤波
高斯多尺度滤波

高斯滤波是低通滤波，利随着 \(\sigma\) 增大，图像的细节（高频部分）逐渐被滤除，图像的尺度依次变大。以 \(\sigma\) 卷积两次相当于以 \(\sqrt{2} \sigma\) 卷积一次。

锐化

原图减低频信息得到高频细节，原图再加上高频细节得到锐化结果。

\[ F+ \alpha (F- F * H) = (1+\alpha)F - \alpha(F*H) = F * ((1+\alpha)I-\alpha H) \]

高斯金字塔

从原图开始，先做高斯滤波，再下采样到一半大小，不断重复，可以构建高斯金字塔。为了避免信号混叠，所以先高斯滤波，降低图像频率，再下采样。

高斯金字塔（左列）
高斯金字塔（左列）

拉普拉斯金字塔

Canny 边缘检测

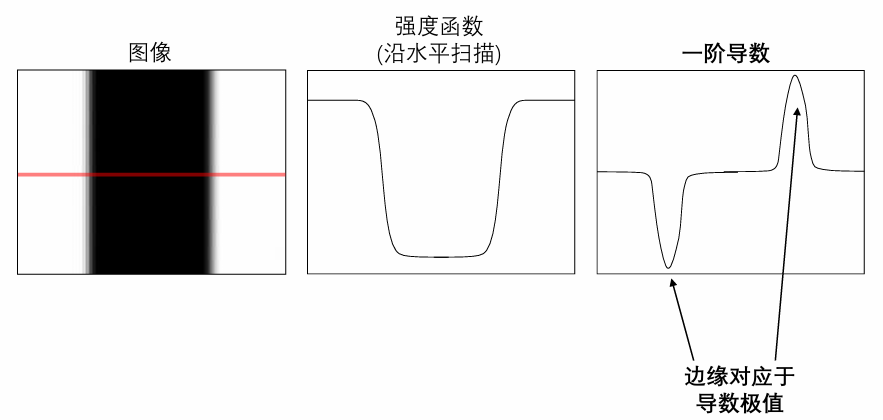
边缘的特征
边缘的特征

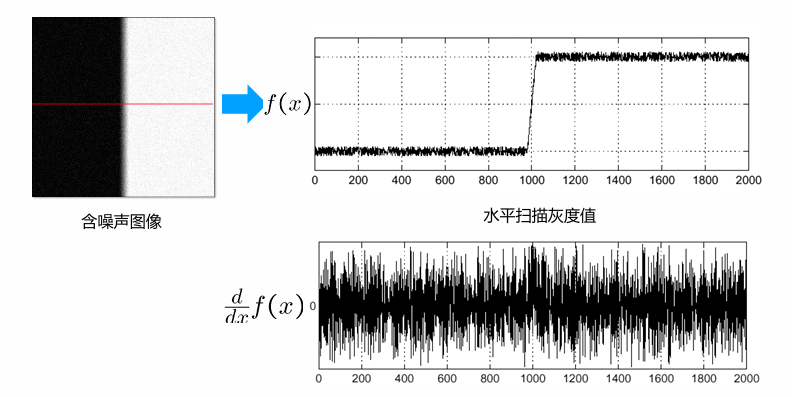
边缘对应图像导数的极值，但求导前应该先滤掉噪声（高斯滤波）。

Noise
Noise

两步合成一步，使用高斯导数做滤波，Sobel 算子是高斯导数的近似

  • 检测垂直边缘：

    \[ S_x=\frac{1}{8}\begin{bmatrix} -1,&0,&1\\ -2,&0,&2\\ -1,&0,&1 \end{bmatrix} \]

  • 检测水平边缘：

    \[ S_y=\frac{1}{8}\begin{bmatrix} 1,&2,&1\\ 0,&0,&0\\ -1,&-2,&-1 \end{bmatrix} \]

Sobel 算子的标准定义省略了 \(\dfrac{1}{8}\) 项，不会对边缘检测产生影响，如果要得到正确的梯度幅值，\(\dfrac{1}{8}\) 项是必须的。

非极大值抑制
非极大值抑制

之前的滤波导致边缘模糊，所以沿梯度的方向抑制非极大值。然后设两个阈值 \(t<T\)，有如下三种情况：

  • \(R>T\): 强边缘
  • \(t<R<T\): 弱边缘
  • \(R<t\): 非边缘

强边缘是边缘，弱边缘仅在与强边缘连接时才是边缘。

总结

  1. 用高斯导数做滤波，获得梯度的幅值与方向
  2. 沿梯度方向进行非极大值抑制
  3. 连接与滞后阈值化：定义两个阈值，使用高阈值寻找边缘曲线的起点，用低阈值确定后继点

Harris 角点检测

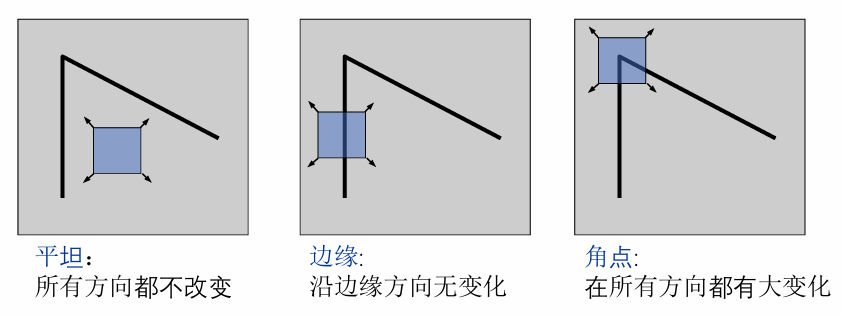
角点特征：高曲率边界点、线交叉点、高显著性点，主要用于图像的特征匹配、特征追踪、机器人导航等领域。

检查一个窗口内像素的变化，来寻找特征。

特征的质量
特征的质量

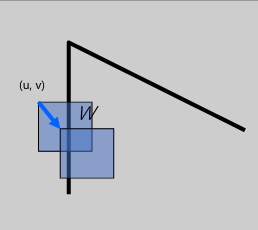
将窗口 \(W\) 平移 \((u,v)\)，比较平移前后窗口 \(W\) 内每个像素的差异平方和（SSD）

SSD
SSD

\[ E(u,v)=\sum_{(x,y)\in W} \bigg[ I(x+u,y+v)-I(x,y) \bigg]^2 \]

考虑 \(I(x+u,y+v) \approx I(x,y) + uI_x + vI_y\) （\(I_x,I_y\) 是图像对 \(x,y\) 的偏导），所以

\[ \begin{align} E(u,v) &\approx \sum_{(x,y)\in W} \bigg[ uI_x + vI_y \bigg]^2\\ \\ &=Au^2 + 2Buv + Cv^2\\ \\ &= \begin{bmatrix} u &v \end{bmatrix} \begin{bmatrix} A &B\\ B &C \end{bmatrix} \begin{bmatrix} u\\ v \end{bmatrix} \end{align} \]

其中

\[ A = \sum_{(x,y)\in W} I_x^2 , \quad B = \sum_{(x,y)\in W} I_xI_y, \quad C = \sum_{(x,y)\in W} I_y^2 \]

记

\[ H=\begin{bmatrix} A &B\\ B &C \end{bmatrix}= \sum_{(x,y)\in W} \begin{bmatrix} I_x^2 &I_xI_y\\ I_xI_y &I_y^2 \end{bmatrix} \]

实际应用中，直接计算图像的导数，容易受噪声的影响，所以我们通常会根据每个点到中心像素的距离对导数进行加权，例如使用高斯函数

\[ H= \sum_{(x,y)\in W} w(x,y) \begin{bmatrix} I_x^2 &I_xI_y\\ I_xI_y &I_y^2 \end{bmatrix} \]

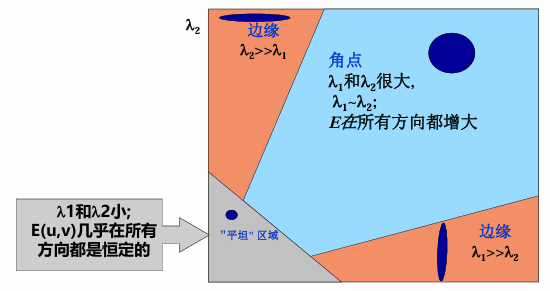
求出两个特征值和特征向量

\[ \begin{align} Hx_{\text{max}}&=\lambda_{\text{max}} x_{\text{max}}\\ Hx_{\text{min}}&=\lambda_{\text{min}} x_{\text{min}} \end{align} \]

分别对应增幅最快和最慢的两个方向，以及对应的变化幅度。

特征值的意义
特征值的意义

为了减少计算，使用另一个公式来判断

\[ \begin{align} C &= \lambda_1 \lambda_2 - \alpha(\lambda_1+\lambda_2)^2\\ &=\det(H) - \alpha \cdot \mathrm{tr}(H)^2 \end{align} \]

其中 \(\alpha\) 是个经验常数。

公式含义
公式含义

具体流程

  1. 计算图像中每个点的梯度
  2. 计算每个点的 \(\begin{bmatrix}I_x^2 &I_xI_y\\I_xI_y &I_y^2\end{bmatrix}\)，然后进行窗口大小的高斯滤波得到 \(H\)
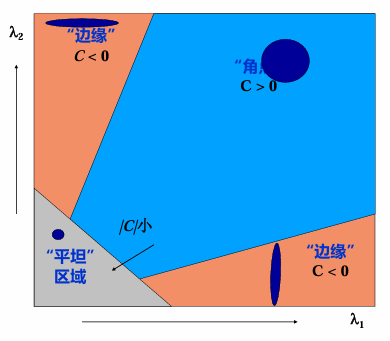
  3. 计算 \(C =\det(H) - \alpha \cdot \mathrm{tr}(H)^2\)
  4. 查找具有较大响应 \(C > \text{threshold}\) 且是局部最大值的点

Harris 角点特征

  • 平移不变性
  • 旋转不变性
  • 亮度变化不变性
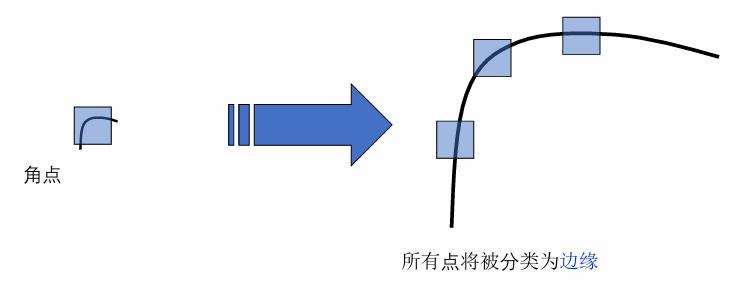
  • 不具有缩放不变性

不具有缩放不变性
不具有缩放不变性

尺度不变特征变换

尺度不变特征变换（Scale Invariant Feature Transform，SIFT）

  • 特征稳定。具有平移、旋转、尺度不变性，并且可以在一定程度上避免 遮挡和噪声等干扰

线性最小二乘法

对于超定（over-determined）非齐次线性方程组 \(\mathbf{A} \mathbf{x}=\mathbf{b}\)，需要找到 \(\mathbf{x}\) 使得 \(\|\mathbf{A} \mathbf{x}-\mathbf{b}\|^2\) 最小，解法是

\[ \mathbf{A}^T\mathbf{A}\mathbf{x}=\mathbf{A}^T\mathbf{b} \]

所以

\[ \mathbf{x}=(\mathbf{A}^T\mathbf{A})^{-1} \mathbf{A}^T\mathbf{b} \]

对于超定齐次线性方程组 \(\mathbf{A} \mathbf{x}=0\)，希望最小化 \(\|\mathbf{A} \mathbf{x}\|^2\) 同时 \(\mathbf{x} \ne 0\)，可以对 \(\mathbf{A}\) 做 SVD

\[ \mathbf{U}\mathbf{\Sigma}\mathbf{V}^T \mathbf{x} = 0 \]

其中 \(\mathbf{U}\) 是酉矩阵，所以上式相当于 \(\mathbf{\Sigma}\mathbf{V}^T \mathbf{x} = 0\)。令 \(\mathbf{y}=\mathbf{V}^T \mathbf{x}\)，得到

\[ \begin{align} \| \mathbf{\Sigma} \mathbf{y} \|^2 &= \mathbf{y}^T \mathbf{\Sigma}^T \mathbf{\Sigma} \mathbf{y}\\ \\ &= \begin{bmatrix} y_1 &y_2 &\cdots &y_n \end{bmatrix} \begin{bmatrix} \sigma_1^2 \\ &\sigma_2^2\\ && \ddots\\ &&& \sigma_n^2 \end{bmatrix} \begin{bmatrix} y_1\\ y_2\\ \vdots\\ y_n \end{bmatrix}\\ \\ &= \sum_{i=1}^n \sigma_i^2 y_i^2 \end{align} \]

已知奇异值 \(\sigma_1 \ge \sigma_2 \ge \cdots \ge \sigma_n \ge 0\)，所以 \(\mathbf{y}=(0,0,\cdots,y_n)^T\) 时，\(\| \mathbf{\Sigma} \mathbf{y} \|^2\) 最小。

\[ \mathbf{x} = \mathbf{V} \mathbf{y} = \begin{bmatrix} \mathbf{v_1} &\mathbf{v_2} &\cdots &\mathbf{v_n}\end{bmatrix}\begin{bmatrix} 0\\ 0\\ \vdots\\ y_n \end{bmatrix}=y_n \mathbf{v_n} \]

把系数 \(y_n\) 除掉后也同样是原方程的解。所以 \(\mathbf{A} \mathbf{x}=0\) 的最小二乘解是 \(\mathbf{A}\) SVD 后 \(\mathbf{V}\) 矩阵的最后一列向量（\(\mathbf{V}^T\) 的最后一行向量）。

非线性最小二乘法

对于单应映射（使用齐次坐标）

\[ \begin{bmatrix} h_{00} &h_{01} &h_{02}\\ h_{10} &h_{11} &h_{12}\\ h_{20} &h_{21} &h_{22}\\ \end{bmatrix} \begin{bmatrix} x_i\\ y_i\\ 1 \end{bmatrix} \simeq \begin{bmatrix} x_i'\\ y_i'\\ 1 \end{bmatrix} \]

实际上

\[ \begin{align} x_i' &= \frac{h_{00}x_i + h_{01}y_i + h_{02}}{h_{20}x_i + h_{21}y_i + h_{22}}\\ \\ y_i' &= \frac{h_{10}x_i + h_{11}y_i + h_{12}}{h_{20}x_i + h_{21}y_i + h_{22}} \end{align} \]

是非线性的，转化为线性方程

\[ \begin{align} (h_{00}x_i + h_{01}y_i + h_{02}) - x_i'(h_{20}x_i + h_{21}y_i + h_{22}) &= 0\\ \\ (h_{10}x_i + h_{11}y_i + h_{12}) - y_i'(h_{20}x_i + h_{21}y_i + h_{22}) &= 0 \end{align} \]

记 \(\mathbf{p}_i=(x_i,y_i,1)^T\)，写成矩阵形式

\[ \begin{bmatrix} \mathbf{p}_i &\mathbf{0} &-x_i' \mathbf{p}_i\\ \mathbf{0} &\mathbf{p}_i &-y_i' \mathbf{p}_i \end{bmatrix} \begin{bmatrix} h_{00}\\ h_{01}\\ h_{02}\\ h_{10}\\ h_{11}\\ h_{12}\\ h_{20}\\ h_{21}\\ h_{22}\\ \end{bmatrix} = \mathbf{0} \]

推广

\[ \begin{bmatrix} \mathbf{p}_1 &\mathbf{0} &-x_1' \mathbf{p}_1\\ \mathbf{0} &\mathbf{p}_1 &-y_1' \mathbf{p}_1\\ &\vdots\\ \mathbf{p}_n &\mathbf{0} &-x_n' \mathbf{p}_n\\ \mathbf{0} &\mathbf{p}_n &-y_n' \mathbf{p}_n\\ \end{bmatrix} \begin{bmatrix} h_{00}\\ h_{01}\\ h_{02}\\ h_{10}\\ h_{11}\\ h_{12}\\ h_{20}\\ h_{21}\\ h_{22}\\ \end{bmatrix} = \mathbf{0} \]

第一个矩阵记为 \(\mathbf{A}\) 是 \(2n \times 9\) 大小的，第二个矩阵记为 \(\mathbf{h}\) 是 \(9 \times 1\) 大小的。

图像配准

最小二乘

  • 特征提取
  • 特征匹配
  • 使用匹配集计算 A 到 B 单应映射的最小二乘解

RANSAC

随机抽样一致算法（RANdom SAmple Consensus）。

  • 特征提取
  • 特征匹配
  • 随机抽几个匹配后的样本，计算 A 到 B 单应映射的最小二乘解
  • 利用刚才的解变换 A 到 B'，找到 B 和 B‘ 差距小于某个阈值的所有特征，这组特征称为内点（inliers）
  • 重复抽样几次，选择长度最大的 inliers
  • 利用 inliers 计算 A 到 B 单应映射的最小二乘解

参考