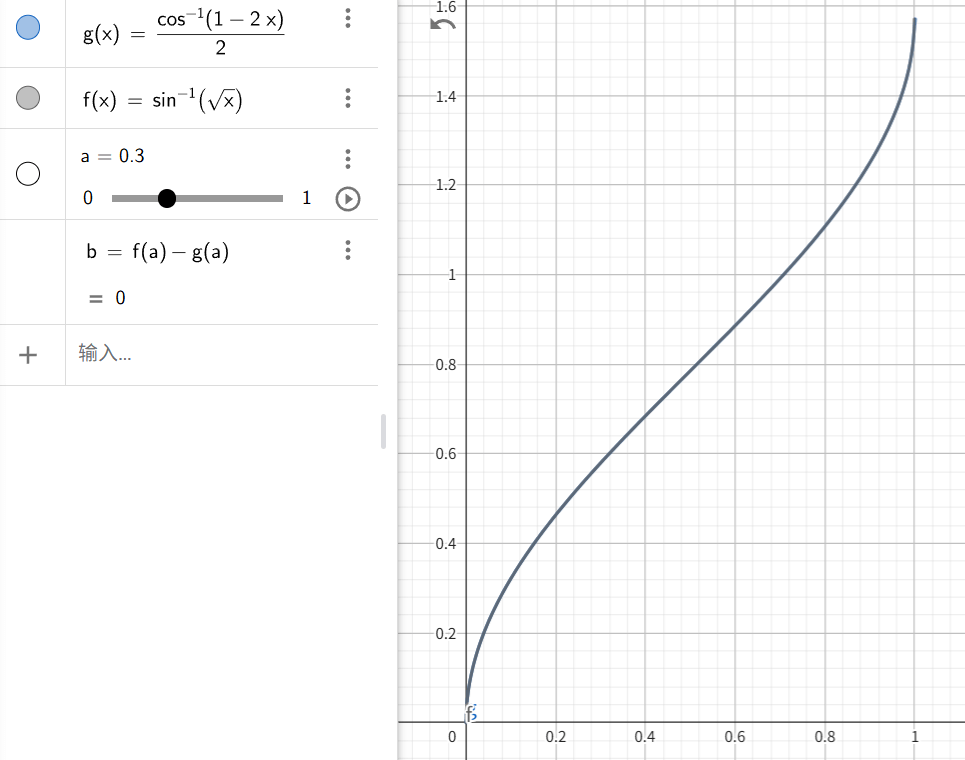根据指定分布采样
根据指定分布采样，也可以理解为生成指定分布的随机数。
逆变换采样
逆变换采样（Inverse Transform Sampling）使用 \([0,1]\) 的均匀分布来生成指定分布的随机数。假设我们要生成服从 \(f(x)\) 分布的随机数。其 CDF 为
\[ F(x)=\int_{-\infty}^{+\infty} f(x) \mathrm{d}x \]
我们的目标是找到一个单调递增的转换函数 \(T(x)\)，使得对于 \(X \sim U[0,1]\)，有 \(T(X) \sim f(x)\)。根据 CDF 的定义
\[ F(x)=P(T(X) \le x)=P(X \le T^{-1}(x)) \]
又因为 \(X \sim U[0,1]\)，所以
\[ P(X \le T^{-1}(x))=T^{-1}(x) \]
联立前两个式子，得到
\[ T(x)=F^{-1}(x) \]
因此，只要将 \([0,1]\) 上均匀分布的随机数输入到 \(F^{-1}(x)\) 中，就能得到服从 \(f(x)\) 分布的随机数。
拒绝采样
常用采样方法
大多数采样方法都是一个套路：
- 确定 PDF 并 变换 到合适的坐标系
- 计算各变量的边缘概率密度
- 计算 CDF
- 使用逆变换采样
注意
在与 蒙特卡罗方法 结合使用时，假设要估计 \(E \left( \dfrac{f(X)}{p(X)} \right)\)，有时我们会采样 \(Y \sim p_Y(y)\)，再变换得到 \(X=g(Y)\)。此时，\(p\) 分布和 \(p_Y\) 分布是不同的！必须算雅可比行列式，根据 \(p_Y\) 得到 \(p\) 的表达式，再带入到 \(\dfrac{f(X)}{p(X)}\)。写代码时一定要注意！
单位圆上均匀采样
利用极坐标生成采样点 \((r,\theta)\)。一个典型的错误是让 \(r\) 和 \(\theta\) 服从均匀分布，得到下图左边的结果，采样点在中心更加密集，并不均匀！
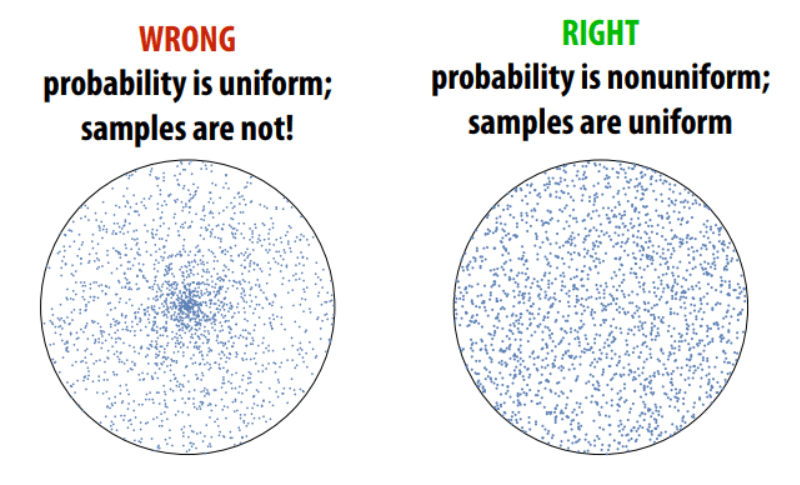圆上均匀采样
应该让圆上单位面积被采样的概率相等，所以 PDF 为
\[ p(x,y)=\frac{1}{\pi} \]
变换到极坐标为
\[ p(r,\theta)=\frac{r}{\pi} \]
边缘概率密度
\[ \begin{align} p(r) &= \int_0^{2\pi} p(r,\theta) \mathrm{d}\theta = 2r\\ p(\theta) &= \int_0^1 p(r,\theta) \mathrm{d}r = \frac{1}{2\pi} \end{align} \]
计算 CDF
\[ \begin{align} P(r) &= \int_0^r p(r) \mathrm{d}r = r^2\\ P(\theta) &= \int_0^\theta p(\theta) \mathrm{d}\theta = \frac{\theta}{2\pi} \end{align} \]
使用逆变换采样，若 \(\xi_1,\xi_2\) 为服从 \(U[0,1]\) 的随机数，则
\[ \begin{align} r&=\sqrt{\xi_1}\\ \theta&=2\pi\xi_2 \end{align} \]
单位球上均匀采样
和前面类似，要让单位 立体角 被采样的概率相等，所以 PDF 为
\[ p(\omega)=\frac{1}{4\pi} \]
变换到球面坐标为
\[ p(\theta,\varphi)=\frac{\sin \theta}{4\pi} \]
边缘概率密度
\[ \begin{align} p(\theta)&=\int_0^{2\pi} p(\theta,\varphi) \mathrm{d}\varphi=\frac{1}{2} \sin \theta\\ p(\varphi)&=\int_0^{\pi} p(\theta,\varphi) \mathrm{d}\theta=\frac{1}{2\pi} \end{align} \]
计算 CDF
\[ \begin{align} P(\theta) &= \int_0^\theta p(\theta) \mathrm{d}\theta = \frac{1 - \cos \theta}{2}\\ P(\varphi) &= \int_0^\varphi p(\varphi) \mathrm{d}\varphi = \frac{\varphi}{2\pi} \end{align} \]
使用逆变换采样
\[ \begin{align} \theta&=\arccos (1-2\xi_1)\\ \varphi&=2\pi\xi_2 \end{align} \]
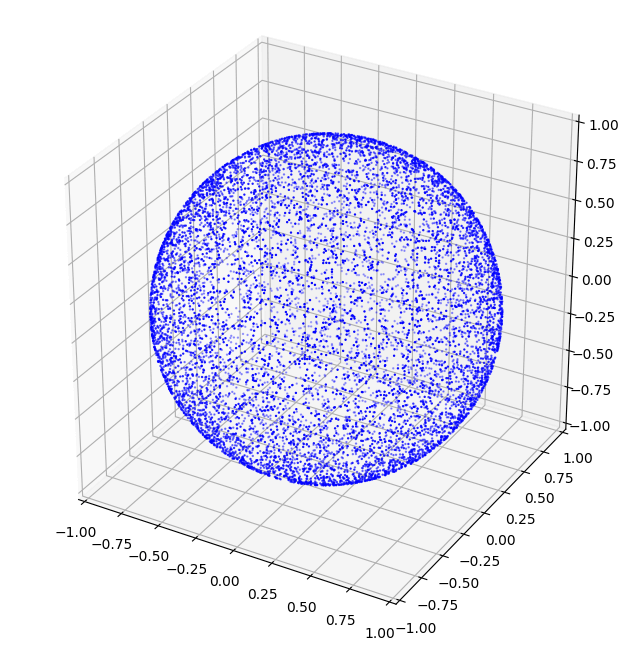单位球上均匀采样
单位半球上均匀采样
和单位球基本一样，只是半球的立体角是 \(2\pi\)，所以逆变换采样为
\[ \begin{align} \theta&=\arccos (1-\xi_1)\\ \varphi&=2\pi\xi_2 \end{align} \]
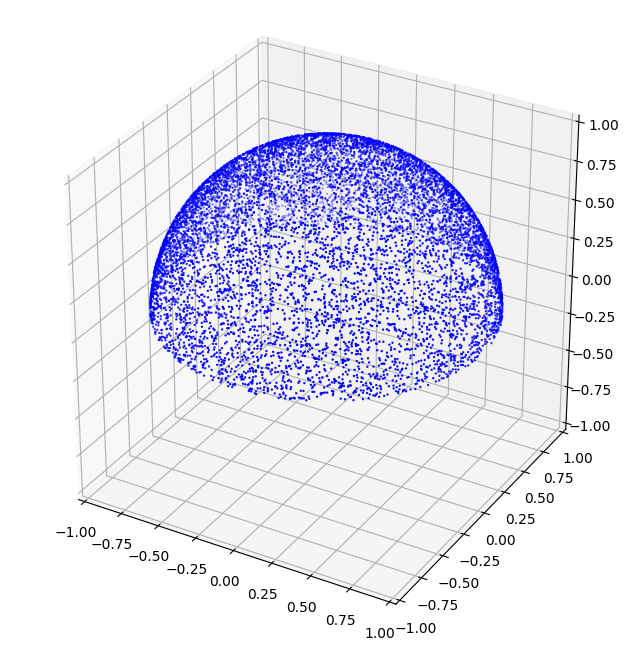单位半球上均匀采样
单位半球上余弦权重采样
图形学中不少公式和夹角余弦有关，比如 渲染方程。根据 重要性采样 理论，余弦权重采样会更好。因为那些公式的自变量都是立体角，所以这里 PDF 的自变量也用立体角。
\[ p(\omega)=\frac{\cos \theta}{k} \]
归一化系数 \(k\) 的值为
\[ \begin{align} k&=\int_{H^2} \cos \theta \mathrm{d}\omega\\ \\ &=\int_0^{2\pi} \displaystyle\int_0^{\pi/2} \cos \theta \sin \theta \mathrm{d}\theta \mathrm{d}\varphi\\ \\ &=\pi \end{align} \]
将 PDF 变换到球面坐标得到
\[ p(\theta,\varphi)=\frac{\cos \theta \sin \theta}{\pi}=\frac{\sin 2 \theta}{2\pi} \]
边缘概率密度
\[ \begin{align} p(\theta)&=\int_0^{2\pi} p(\theta,\varphi) \mathrm{d}\varphi=\sin 2 \theta\\ p(\varphi)&=\int_0^{\pi/2} p(\theta,\varphi) \mathrm{d}\theta=\frac{1}{2\pi} \end{align} \]
计算 CDF
\[ \begin{align} P(\theta) &= \int_0^\theta p(\theta) \mathrm{d}\theta = \frac{1 - \cos 2\theta}{2}\\ P(\varphi) &= \int_0^\varphi p(\varphi) \mathrm{d}\varphi = \frac{\varphi}{2\pi} \end{align} \]
使用逆变换采样
\[ \begin{align} \theta&=\frac{1}{2} \arccos (1-2\xi_1)\\ \varphi&=2\pi\xi_2 \end{align} \]
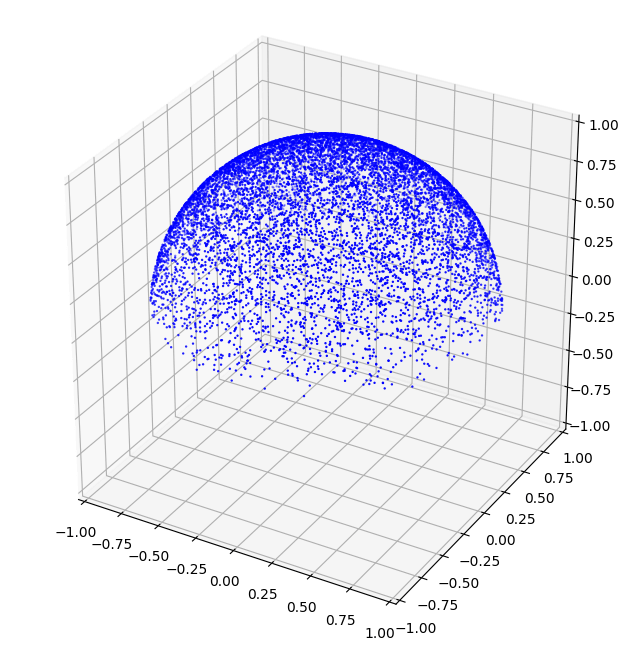单位半球上余弦权重采样
Malley's Method
如果转动视角，从上往下观察余弦权重采样点，会发现它们在平面上的投影是均匀的。
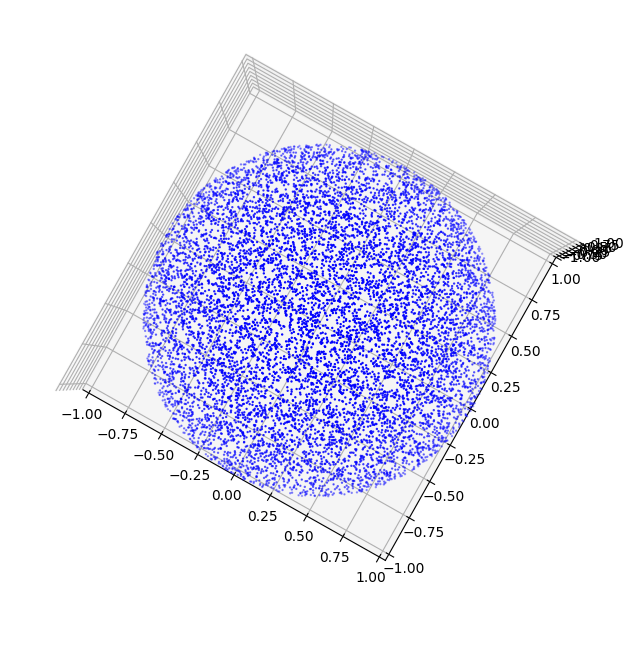Malley's Method
那是否可以反过来，先在单位圆上均匀采样，然后把采样点投影到半球上，得到余弦权重采样点？根据前面的推导，单位圆上的均匀采样点为
\[ \begin{align} r&=\sqrt{\xi_1}\\ \varphi&=2\pi\xi_2 \end{align} \]
投影到单位半球后，对应点的 \(\theta\) 为
\[ \theta=\arcsin \left(\frac{r}{1} \right)=\arcsin(\sqrt{\xi_1}) \]
可以证明
\[ \arcsin(\sqrt{\xi_1}) \equiv \frac{1}{2} \arccos (1-2\xi_1) \]
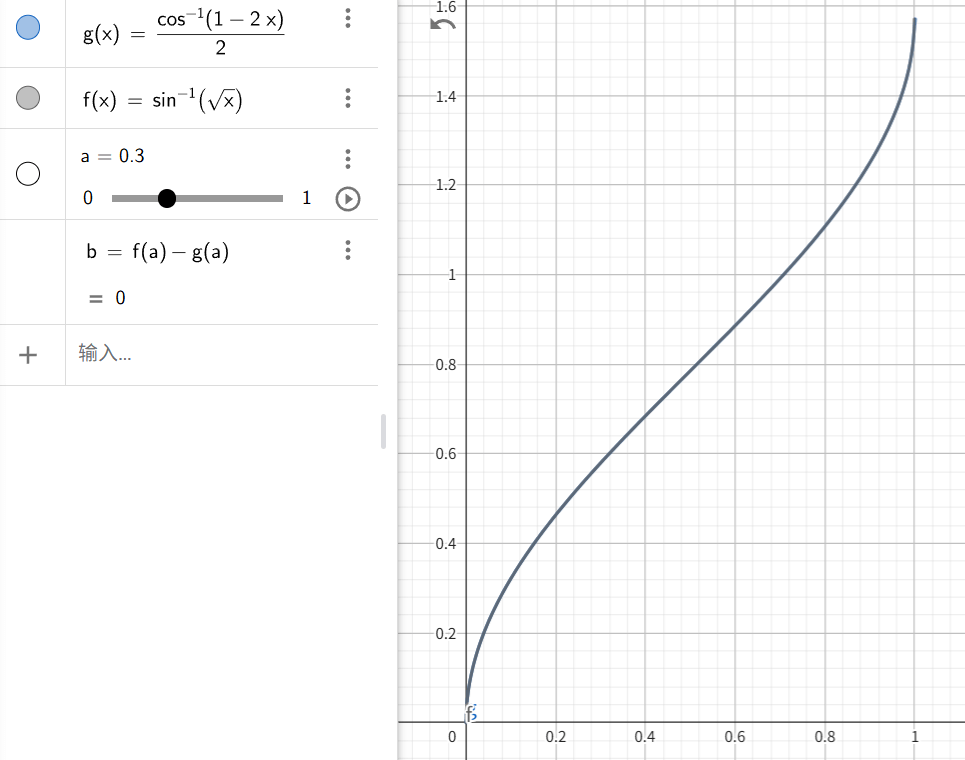函数图像
从绘图结果看也是一样的，所以这种方法是可行的。用这个方法的话，可以更方便地把结果转换到笛卡尔坐标系。
单位半球上 GGX 权重采样
在 NDF 理论 中提到过，如果 \(D(h)\) 是一个 NDF，那么 \(D(h) (n \cdot h)\) 可以当作一个概率密度函数，其中 \(n\) 是表面宏观法线方向，\(h\) 是 half vector。因此，对于 GGX 来说，立体角 PDF 可以使用
\[ p(\omega)=\frac{\alpha^2 \cos \theta}{\pi \left(1 + (\alpha^2-1)\cos^2 \theta \right)^2} \]
其中，\(\cos \theta=(\mathbf{n} \cdot \mathbf{h})\)。将 PDF 变换到球面坐标得到
\[ p(\theta,\varphi)=\frac{\alpha^2 \cos \theta \sin \theta}{\pi \left(1 + (\alpha^2-1)\cos^2 \theta \right)^2} \]
边缘概率密度
\[ \begin{align} p(\theta)&=\int_0^{2\pi} p(\theta,\varphi) \mathrm{d}\varphi=\frac{2\alpha^2 \cos \theta \sin \theta}{\left(1 + (\alpha^2-1)\cos^2 \theta \right)^2}\\ \\ p(\varphi)&=\int_0^{\pi/2} p(\theta,\varphi) \mathrm{d}\theta\\ \\ &=\int_0^{\pi/2} \frac{\alpha^2 \cos \theta \sin \theta \mathrm{d}\theta}{\pi \left(1 + (\alpha^2-1)\cos^2 \theta \right)^2}\\ \\ &\xlongequal{t=\cos^2 \theta}\frac{\alpha^2}{2\pi} \int_0^{1} \frac{\mathrm{d}t}{\left(1 + (\alpha^2-1)t \right)^2}\\ \\ &\xlongequal{u=1+(\alpha^2-1)t}\frac{\alpha^2}{2\pi(\alpha^2-1)} \int_1^{\alpha^2} \frac{\mathrm{d}u}{u^2}\\ \\ &=\frac{\alpha^2}{2\pi(\alpha^2-1)} \cdot \frac{\alpha^2-1}{\alpha^2}\\ \\ &= \frac{1}{2\pi} \end{align} \]
计算 CDF
\[ \begin{align} P(\theta) &= \int_0^\theta p(\theta) \mathrm{d}\theta\\ \\ &=\int_0^\theta \frac{2\alpha^2 \cos \theta \sin \theta \mathrm{d}\theta}{\left(1 + (\alpha^2-1)\cos^2 \theta \right)^2}\\ \\ &\xlongequal{t=\cos^2 \theta}\int_t^1 \frac{\alpha^2 \mathrm{d}t}{\left(1 + (\alpha^2-1)t \right)^2}\\ \\ &\xlongequal{u=1+(\alpha^2-1)t}\frac{\alpha^2}{\alpha^2-1} \int_u^{\alpha^2} \frac{\mathrm{d}u}{u^2}\\ \\ &=\frac{\alpha^2}{\alpha^2-1} \cdot \left( \frac{1}{u} - \frac{1}{\alpha^2} \right)\\ \\ &=\frac{1-\cos^2 \theta}{1+(\alpha^2-1)\cos^2 \theta}\\ \\ P(\varphi) &= \int_0^\varphi p(\varphi) \mathrm{d}\varphi = \frac{\varphi}{2\pi} \end{align} \]
使用逆变换采样
\[ \begin{align} \theta&=\arccos \sqrt{\frac{1-\xi_1}{1+(\alpha^2-1)\xi_1}}\\ \varphi&=2\pi\xi_2 \end{align} \]
从半程向量到入射 / 出射方向
有时候，我们会使用这个分布采样得到 half vector \(h\)，进而计算入射方向 \(i\) 或者出射方向 \(o\)。有必要推导 \(h\) 的分布 \(p_h(h)\) 和出射方向 \(o\) 的分布 \(p_o(o)\) 之间的关系。
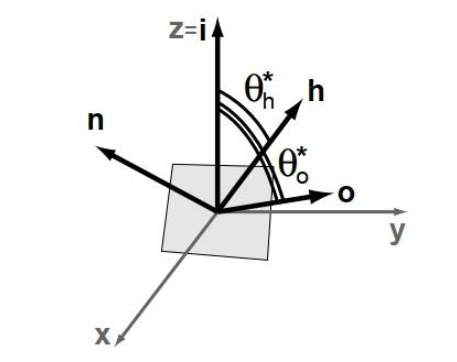球面坐标下的一种简化情况
为了方便，只考虑球面坐标下的一种简化情况。此时入射方向 \(i\) 为 z 轴，\(\theta^*_o = 2\theta^*_h\) 且 \(\varphi^*_o=\varphi^*_h\)。根据 概率密度函数的坐标系变换 规则，在球面坐标中
\[ p_o(o) \sin \theta^*_o = \frac{p_h(h) \sin \theta^*_h}{\left| \det \left( \dfrac{\partial(\theta^*_o,\varphi^*_o)}{\partial(\theta^*_h,\varphi^*_h)} \right) \right|} \]
其中，雅可比行列式
\[ \det \left( \dfrac{\partial(\theta^*_o,\varphi^*_o)}{\partial(\theta^*_h,\varphi^*_h)} \right)=\begin{vmatrix} \dfrac{\partial \theta^*_o}{\partial \theta^*_h} &\dfrac{\partial \theta^*_o}{\partial \varphi^*_h}\\ \dfrac{\partial \varphi^*_o}{\partial \theta^*_h} &\dfrac{\partial \varphi^*_o}{\partial \varphi^*_h}\\ \end{vmatrix}=\begin{vmatrix} 2 &0\\ 0 &1 \end{vmatrix}=2 \]
所以
\[ \begin{align} p_o(o)&=\frac{p_h(h)\sin \theta^*_h}{2\sin \theta^*_o}\\ \\ &=\frac{p_h(h)\sin \theta^*_h}{2\sin 2\theta^*_h}\\ \\ &=\frac{p_h(h)}{4\cos \theta^*_h}\\ \\ &=\frac{p_h(h)}{4 (h \cdot i)}=\frac{p_h(h)}{4 (h \cdot o)} \end{align} \]
入射方向 \(i\) 的公式和这个一样。
参考