字符串排序¶

Key-Indexed Counting¶

用于排序一组字符，例如字符串内部的字符。

利用 count 数组统计字符个数，注意保证 count[0] == 0，计数值要从 count[1] 开始保存
算前缀和，得到每种字符的起始位置
将字符重新填入字符串

假设 a 为字符串，所有字符值都在 [0, R) 内。

int N = a.length;
int R = 256;   // extend ASCII alphabet size
String[] aux = new String[N];

// compute frequency counts
int[] count = new int[R+1];
for (int i = 0; i < N; i++)
    count[a[i]+1]++;

// compute cumulates
for (int r = 0; r < R; r++)
    count[r+1] += count[r];

// move data
for (int i = 0; i < N; i++)
    aux[count[a[i]]++] = a[i];

// copy back
for (int i = 0; i < N; i++)
    a[i] = aux[i];

时间复杂度：\(O(N+R)\)
空间复杂度：\(O(N+R)\)

LSD Radix Sort¶

用于排序多个字符串，从右到左（低位优先），对每一列字符进行 key-indexed couting，然后调整字符串顺序。

public class LSD {
    public static void sort(String[] a, int w) {
        int n = a.length;
        int R = 256;   // extend ASCII alphabet size
        String[] aux = new String[n];

        for (int d = w-1; d >= 0; d--) {
            // sort by key-indexed counting on dth character

            // compute frequency counts
            int[] count = new int[R+1];
            for (int i = 0; i < n; i++)
                count[a[i].charAt(d) + 1]++;

            // compute cumulates
            for (int r = 0; r < R; r++)
                count[r+1] += count[r];

            // move data
            for (int i = 0; i < n; i++)
                aux[count[a[i].charAt(d)]++] = a[i];

            // copy back
            for (int i = 0; i < n; i++)
                a[i] = aux[i];
        }
    }
}

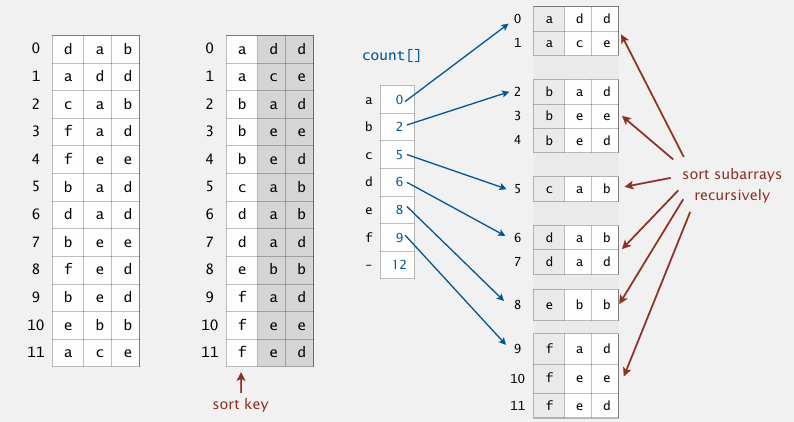
MSD Radix Sort¶

用于排序多个字符串，从左到右（高位优先），对每一列字符进行 key-indexed couting，然后调整字符串顺序。

public class MSD {
    private static final int R      = 256;   // extended ASCII alphabet size
    private static final int CUTOFF =  15;   // cutoff to insertion sort

    // return dth character of s, -1 if d = length of string
    private static int charAt(String s, int d) {
        assert d >= 0 && d <= s.length();
        if (d == s.length()) return -1;
        return s.charAt(d);
    }

    public static void sort(String[] a) {
        int n = a.length;
        String[] aux = new String[n];
        sort(a, 0, n-1, 0, aux);
    }

    // sort from a[lo] to a[hi], starting at the dth character
    private static void sort(String[] a, int lo, int hi, int d, String[] aux) {
        // cutoff to insertion sort for small subarrays
        if (hi <= lo + CUTOFF) {
            insertion(a, lo, hi, d);
            return;
        }

        // compute frequency counts
        int[] count = new int[R+2];
        for (int i = lo; i <= hi; i++) {
            int c = charAt(a[i], d);
            count[c+2]++;
        }

        // transform counts to indices
        for (int r = 0; r < R+1; r++)
            count[r+1] += count[r];

        // distribute
        for (int i = lo; i <= hi; i++) {
            int c = charAt(a[i], d);
            aux[count[c+1]++] = a[i];
        }

        // copy back
        for (int i = lo; i <= hi; i++)
            a[i] = aux[i - lo];

        // recursively sort for each character (excludes sentinel -1)
        for (int r = 0; r < R; r++)
            sort(a, lo + count[r], lo + count[r+1] - 1, d+1, aux);
    }
}

按当前列排序好后，最后一个 for 循环会按这一列的字符分组递归。这一列字符相同的字符串会被分到一组，然后根据后一列排序。

如果拆分的 subarray 都很小，效率会变低，所以 subarray 长度足够小时，改用插入排序
如果相同字符串较多，性能也不好
如果字符串不一样长，可以在字符串后面补 -1，参考 charAt() 方法

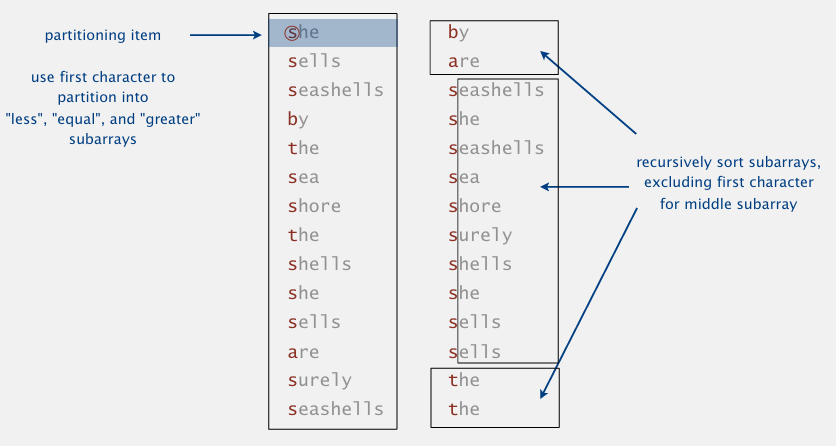
3-Way String Quicksort¶

public class Quick3string {
    private static final int CUTOFF =  15;   // cutoff to insertion sort

    public static void sort(String[] a) {
        StdRandom.shuffle(a);
        sort(a, 0, a.length-1, 0);
    }

    // return the dth character of s, -1 if d = length of s
    private static int charAt(String s, int d) {
        if (d == s.length()) return -1;
        return s.charAt(d);
    }

    // 3-way string quicksort a[lo..hi] starting at dth character
    private static void sort(String[] a, int lo, int hi, int d) {
        // cutoff to insertion sort for small subarrays
        if (hi <= lo + CUTOFF) {
            insertion(a, lo, hi, d);
            return;
        }

        int lt = lo, gt = hi;
        int v = charAt(a[lo], d);
        int i = lo + 1;
        while (i <= gt) {
            int t = charAt(a[i], d);
            if      (t < v) exch(a, lt++, i++);
            else if (t > v) exch(a, i, gt--);
            else              i++;
        }

        // a[lo..lt-1] < v = a[lt..gt] < a[gt+1..hi].
        sort(a, lo, lt-1, d);
        if (v >= 0) sort(a, lt, gt, d+1);
        sort(a, gt+1, hi, d);
    }

    // exchange a[i] and a[j]
    private static void exch(String[] a, int i, int j) {
        String temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

相关文章
算法考试