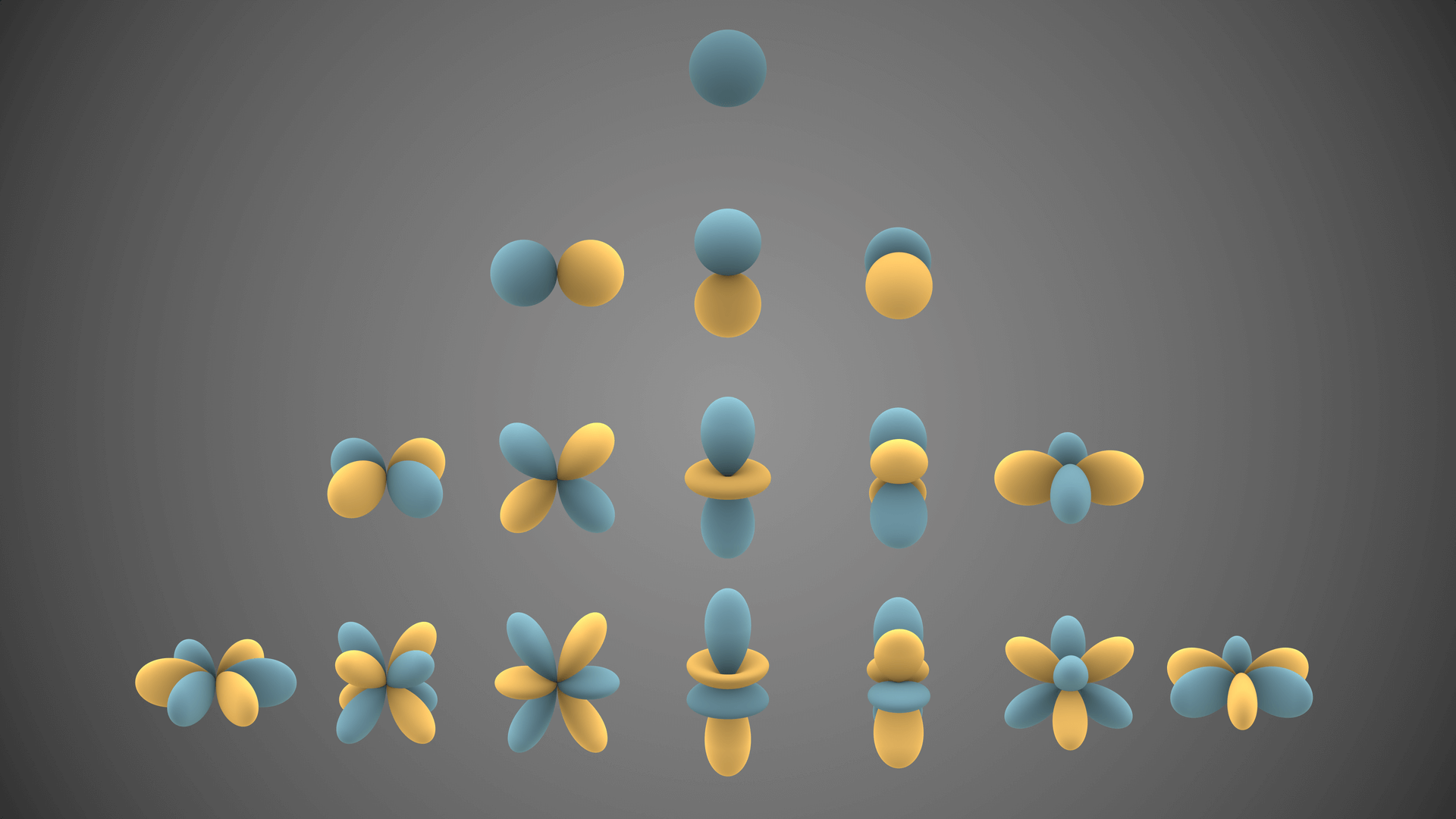跳转至

球谐函数

球谐函数是拉普拉斯方程在球坐标下，角度部分的解，常用于保存低频的数据，例如环境光漫反射。

求解

球坐标系下的 拉普拉斯方程

\[ {\frac{1}{r^{2}}}{\frac{\partial}{\partial r}}\left(r^{2}{\frac{\partial f}{\partial r}}\right)+{\frac{1}{r^{2}\sin\theta}}{\frac{\partial}{\partial\theta}}\left(\sin\theta{\frac{\partial f}{\partial\theta}}\right)+{\frac{1}{r^{2}\sin^{2}\theta}}{\frac{\partial^{2}f}{\partial\varphi^{2}}}=0 \]

先分离 \(f\) 中的变量，令

\[ f\left(r,\theta,\varphi\right)=R\left(r\right)Y\left(\theta,\varphi\right) \]

再代回方程得到

\[ {\frac{Y}{r^{2}}}{\frac{\partial}{\partial r}}\biggl(r^{2}{\frac{\partial R}{\partial r}}\biggr)+{\frac{R}{r^{2}\sin\theta}}{\frac{\partial}{\partial\theta}}\biggl(\sin\theta{\frac{\partial Y}{\partial\theta}}\biggr)+{\frac{R}{r^{2}\sin^{2}\theta}}{\frac{\partial^{2}Y}{\partial\varphi^{2}}}=0 \]

整理一下得到

\[ {\frac{1}{R}}{\frac{\partial}{\partial r}}\biggl(r^{2}{\frac{\partial R}{\partial r}}\biggr)=-{\frac{1}{Y\sin\theta}}{\frac{\partial}{\partial\theta}}\biggl(\sin\theta{\frac{\partial Y}{\partial\theta}}\biggr)-{\frac{1}{Y\sin^{2}\theta}}{\frac{\partial^{2}Y}{\partial\varphi^{2}}} \]

注意到，等式左边只和 \(r\) 有关，等式右边只和 \(\theta,\varphi\) 有关，只有两边同时等于一个常数时，等式才能成立。通常，令这个常数等于 \(l(l+1)\)，于是

\[ {\frac{1}{R}}{\frac{\partial}{\partial r}}\biggl(r^{2}{\frac{\partial R}{\partial r}}\biggr)=-{\frac{1}{Y\sin\theta}}{\frac{\partial}{\partial\theta}}\biggl(\sin\theta{\frac{\partial Y}{\partial\theta}}\biggr)-{\frac{1}{Y\sin^{2}\theta}}{\frac{\partial^{2}Y}{\partial\varphi^{2}}}=l(l+1) \]

可以被拆成两个方程，这里只考虑和角度有关的 \(Y\left(\theta,\varphi\right)\)

\[ {\frac{1}{\sin\theta}}{\frac{\partial}{\partial\theta}}\biggl(\sin\theta{\frac{\partial Y}{\partial\theta}}\biggr)+{\frac{1}{\sin^{2}\theta}}{\frac{\partial^{2}Y}{\partial\varphi^{2}}}+l\left(l+1\right)Y=0 \]

再用一次前面的套路，进一步分离变量，令

\[ Y\left(\theta,\varphi\right)=\Theta\left(\theta\right)\Phi\left(\varphi\right) \]

代入方程得到

\[ \frac{\Phi}{\sin\theta}\frac{\partial}{\partial\theta}\biggl(\sin\theta\frac{\partial\Theta}{\partial\theta}\biggr)+\frac{\Theta}{\sin^{2}\theta}\frac{\partial^{2}\Phi}{\partial\varphi^{2}}+l\left(l+1\right)\Theta\Phi=0 \]

整理一下得到

\[ \frac{\sin\theta}{\Theta}\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial\Theta}{\partial\theta}\right)+l\left(l+1\right)s\mathrm{in}^{2}\theta=-\frac{1}{\Phi}\frac{\partial^{2}\Phi}{\partial\varphi^{2}} \]

注意到，等式左边只和 \(\theta\) 有关，等式右边只和 \(\varphi\) 有关，只有两边同时等于一个常数时，等式才能成立。通常，令这个常数等于 \(m^2\)，于是又变成了两个方程

\[ \frac{\partial^{2}\Phi}{\partial\varphi^{2}}=-m^2\Phi \]
\[ \frac{1}{\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial\Theta}{\partial\theta}\right)+\left[l\left(l+1\right)-\frac{m^2}{\sin^{2}\theta}\right]\Theta=0 \]

第一个方程是 齐次线性微分方程，可以用特征方程求解。第二个方程，令 \(x=\cos\theta\) 可以转化为 \(l\) 次连带勒让德方程

\[ \left(1-x^{2}\right)\frac{\partial^{2}\Theta}{\partial x^{2}}-2x\frac{\partial\Theta}{\partial x}+\left[l\left(l+1\right)-\frac{m^{2}}{1-x^{2}}\right]\Theta=0 \]

最后，把解出来的 \(\Phi\) 和 \(\Theta\) 乘起来，就得到完整的解了，具体的公式不写了

\[ Y_{l}^{m}(\theta,\varphi), \quad l \in \mathbb{N}, -l \le m \le l \]

其中，\(l\) 被称为 band，从 \(0\) 开始。每个 band 有 \(2l+1\) 个函数。前 \(n\) 个 band 有 \(n^2\) 个函数。不过，现在 \(Y_{l}^{m}(\theta,\varphi)\) 中还包含不确定的积分常数，我们可以人为给定一个归一化条件，解出常数的值

\[ \int_{S^2} Y_{l}^{m}(\omega) Y_{l}^{m*}(\omega) \mathrm{d}\omega=\int_{S^2} \left| Y_{l}^{m}(\omega) \right|^2 \mathrm{d}\omega=1 \]

上式是在整个球面上做立体角积分，表示 \(Y_{l}^{m}(\theta,\varphi)\) 自己和自己的点乘等于 \(1\)，即模长的平方为 \(1\)。注意 \(Y_{l}^{m}(\theta,\varphi)\) 是一个复函数，点乘需要共轭。

前 4 个 band
前 4 个 band

中间的一列函数，即 \(m=0\) 的函数 \(Y_{l}^{0}(\theta,\varphi)\)，也被称为 Zonal Harmonics（ZH），它们关于 \(z\) 轴旋转对称。

基函数表

之前推导的是复数域的基函数，但在图形学中常用实数域的版本，下面列出的是前 9 个归一化（\(r=1\)）的系数。1

\(l \backslash m\) \(-2\) \(-1\) \(0\) \(1\) \(2\)
\(0\) \({\dfrac{1}{2}}{\sqrt{\dfrac{1}{\pi}}}\)
\(1\) \({\sqrt{\dfrac{3}{4\pi}}}\cdot y\) \({\sqrt{\dfrac{3}{4\pi}}}\cdot z\) \({\sqrt{\dfrac{3}{4\pi}}\cdot x}\)
\(2\) \({\dfrac{1}{2}}{\sqrt{\dfrac{15}{\pi}}}\cdot x y\) \({\dfrac{1}{2}}{\sqrt{\dfrac{15}{\pi}}}\cdot yz\) \(\dfrac{1}{4}\sqrt{\dfrac{5}{\pi}}\cdot (3z^{2}-1)\) \({\dfrac{1}{2}}{\sqrt{\dfrac{15}{\pi}}}\cdot xz\) \(\dfrac{1}{4}\sqrt{\dfrac{15}{\pi}}\cdot (x^{2}-y^{2})\) 
// SH Basis coefs
#define SHBasis0 0.28209479177387814347f // {0, 0} : 1/2 * sqrt(1/Pi)
#define SHBasis1 0.48860251190291992159f // {1, 0} : 1/2 * sqrt(3/Pi)
#define SHBasis2 1.09254843059207907054f // {2,-2} : 1/2 * sqrt(15/Pi)
#define SHBasis3 0.31539156525252000603f // {2, 0} : 1/4 * sqrt(5/Pi)
#define SHBasis4 0.54627421529603953527f // {2, 2} : 1/4 * sqrt(15/Pi)

void GetSH9Basis(float3 N, out float basis[9])
{
    basis[0] = SHBasis0;
    basis[1] = SHBasis1 * N.y;
    basis[2] = SHBasis1 * N.z;
    basis[3] = SHBasis1 * N.x;
    basis[4] = SHBasis2 * N.x * N.y;
    basis[5] = SHBasis2 * N.y * N.z;
    basis[6] = SHBasis3 * (3.0 * N.z * N.z - 1.0);
    basis[7] = SHBasis2 * N.x * N.z;
    basis[8] = SHBasis4 * (N.x * N.x - N.y * N.y);
}

性质

下面都讨论实数域球谐基函数 \(Y_{l}^{m}(\theta,\varphi)\) 的性质。

正交归一化

\[ \int_{S^2} Y_{l}^{m}(\omega) Y_{l'}^{m'}(\omega) \mathrm{d}\omega=\delta_{ll'}\delta_{mm'} \]

其中，\(\delta_{ij}\) 是克罗内克 \(\delta\) 函数（Kronecker delta）。上式就是两个基函数的点乘，当 \(l=l' \wedge m=m'\) 时为 \(1\)，其余情况为 \(0\)。这说明基函数是两两正交，且归一化的。

投影

\[ \begin{align} f_l^m&=\int_{S^2} f(\omega) Y_{l}^{m}(\omega) \mathrm{d}\omega\\ \\ &=\int_0^{2\pi} \int_0^{\pi} f(\theta,\varphi) Y_{l}^{m}(\theta,\varphi) \sin \theta \mathrm{d}\theta \mathrm{d}\varphi \end{align} \]

卷积

如果卷积核函数 \(h(z)\) 关于 \(z\) 轴旋转对称，即球谐系数中只有 \(h_l^0\) 不为 \(0\)，则

\[ (h * f)_{l}^{m}=\sqrt{\frac{4\pi}{2l+1}}h_{l}^{0}f_{l}^{m} \]

余弦

Ringing

参考

  1. Table of spherical harmonics - Wikipedia ↩