实信号与复信号的频谱实验¶
大二下,信号与系统作业。
- 画出 \(\cos(\omega_0 t + \phi)\) 的频谱,其中 \(\omega_0\) 的数值分别为 \(1,3,6\);\(\phi\) 的数值分别为 \(15^\circ, -30^\circ, 60^\circ\)。
- 画出 \(\exp(j(\omega_0 t + \phi))\) 的频谱,其中 \(\omega_0\) 的数值分别为 \(1,3,6\);\(\phi\) 的数值分别为 \(15^\circ, -30^\circ, 60^\circ\)。
- 将第二问中的 3 个复信号两两组合,写出获得的 3 个信号的表达式,分别画出其实部信号的频谱。
前置准备¶
# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
# 题目中的 omega 和 phi 的取值
omega_values = [1, 3, 6]
phi_values = list(map(np.radians, [15, -30, 60]))
因为题目给的函数对应的 \(F(j\omega)\) 只在某几个点处有取值,所以可以用 DFT 计算它。
先在一个周期 \([0, 2\pi)\) 里以 \(1000\) 的采样率进行均匀采样,把函数 \(f\) 离散化,再用 FFT 算法计算其 DFT。需要注意的是,由于采样率为 \(1000\),所以实际上是在对 \(f \left(\dfrac{k}{1000} \right)\) 做 DFT,算出来的结果需要除掉采样率做修正。
TOTAL_TIME = 2 * np.pi # 一个周期
SAMPLE_RATE = 1000 # 采样率
# 对函数进行傅里叶变换
def compute_fourier_transform(f):
t = np.linspace(0, TOTAL_TIME, int(SAMPLE_RATE * TOTAL_TIME),
endpoint=False)
samples = f(t)
freq = np.fft.fftfreq(len(samples), 1 / SAMPLE_RATE)
freq *= 2 * np.pi # 转换为角频率
dft = np.fft.fft(samples) / SAMPLE_RATE
nonzero = np.where(np.abs(dft) > 1e-10)
return freq[nonzero], dft[nonzero]
下面写了一个 plot_signals 函数,用于同时绘制多个信号的频谱。
class SignalInfo:
def __init__(self, title, f):
self.title = title
self.f = f # 关于时间的函数
# 绘制频谱图
def plot_signals(signals: list[SignalInfo]):
plt.figure(figsize=(4 * len(signals), 4 * 2))
for i, sig in enumerate(signals):
freq, values = compute_fourier_transform(sig.f)
magnitude = np.abs(values)
phase = np.angle(values, deg=True)
# 绘制幅度
plt.subplot(2, len(signals), i + 1)
plt.stem(freq, magnitude)
plt.title(sig.title)
plt.ylabel(r'Magnitude')
plt.grid(True)
for x, y in zip(freq, magnitude):
plt.annotate(f'{y:.2f}', xy=(x, y),
ha='center', va='bottom', color='red')
# 绘制相位
plt.subplot(2, len(signals), i + 1 + len(signals))
plt.stem(freq, phase)
plt.xlabel(r'Angular Frequency (rad/s)')
plt.ylabel(r'Phase (deg)')
plt.grid(True)
for x, y in zip(freq, phase):
plt.annotate(f'{y:.2f}', xy=(x, y),
ha='center', va='bottom', color='red')
plt.tight_layout()
plt.show()
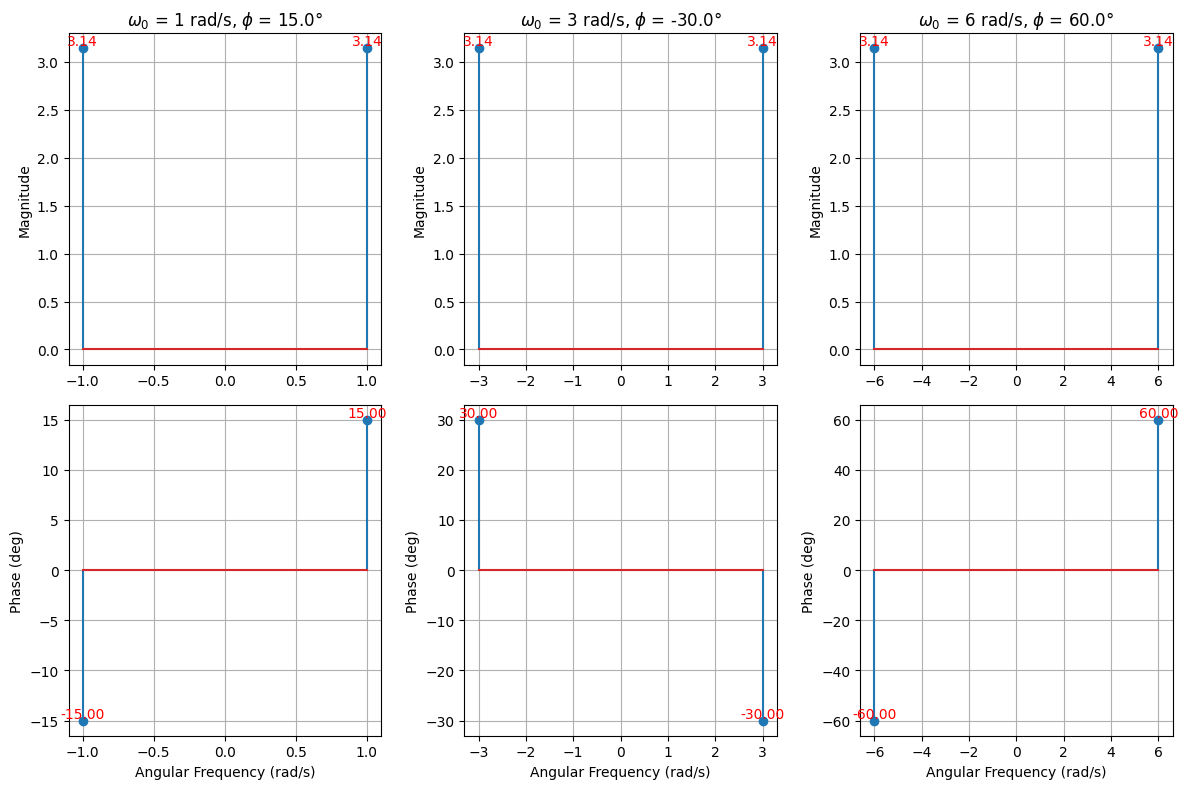
第一问¶
\[ \cos(\omega_0 t + \phi) \longleftrightarrow \pi \left[ \delta(\omega+\omega_0) e^{-j\phi} + \delta(\omega-\omega_0) e^{j\phi} \right] \]
plot_signals([
SignalInfo(
title=rf'$\omega_0$ = {omega} rad/s, '
rf'$\phi$ = {np.round(np.degrees(phi))}°',
f=lambda t, omega=omega, phi=phi: np.cos(omega * t + phi)
)
for omega, phi in zip(omega_values, phi_values)
])
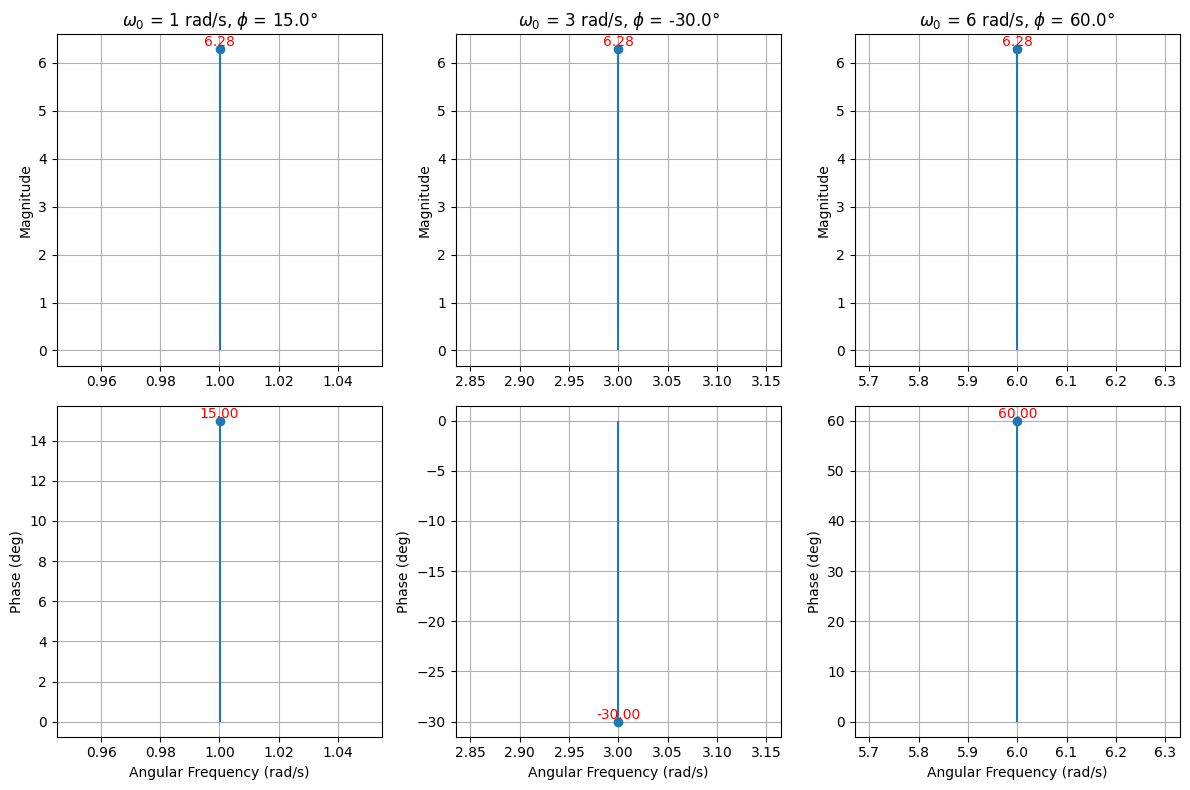
第二问¶
\[ e^{j(\omega_0 t + \phi)} \longleftrightarrow 2\pi \delta(\omega-\omega_0) e^{j\phi} \]
plot_signals([
SignalInfo(
title=rf'$\omega_0$ = {omega} rad/s, '
rf'$\phi$ = {np.round(np.degrees(phi))}°',
f=lambda t, omega=omega, phi=phi: np.exp(1j * (omega * t + phi))
)
for omega, phi in zip(omega_values, phi_values)
])
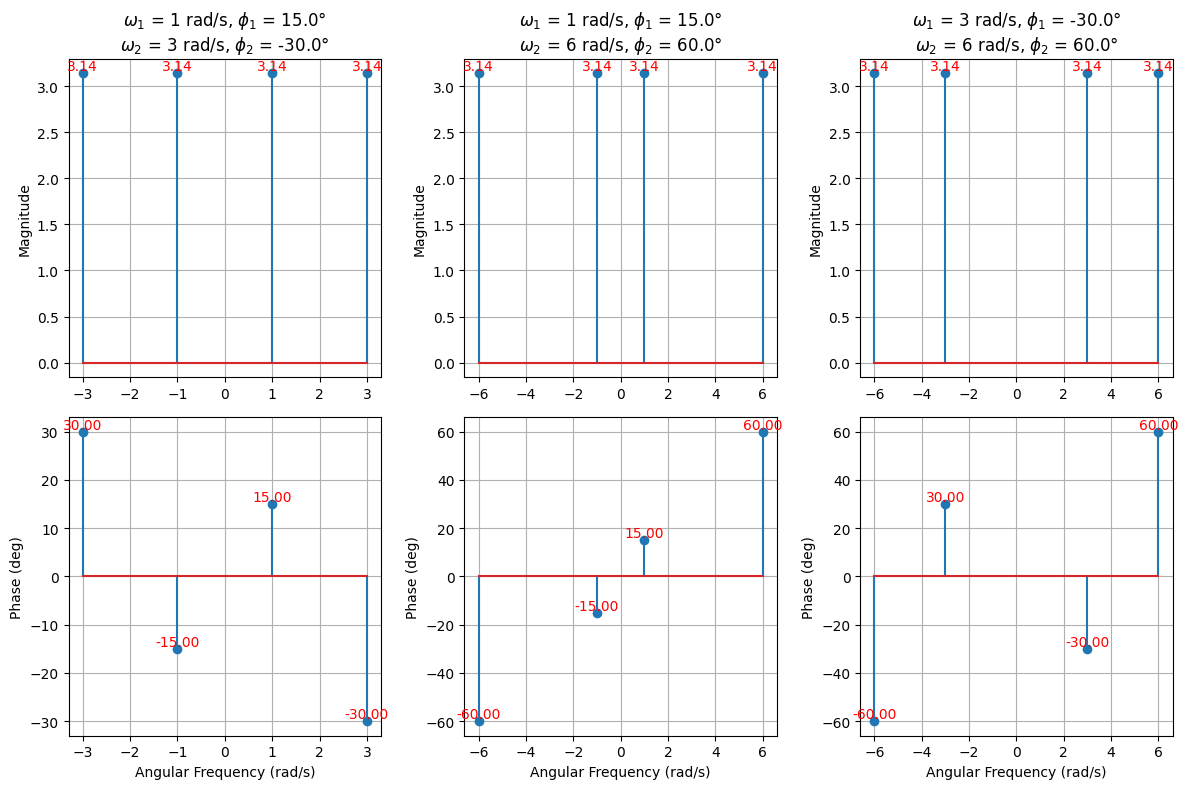
第三问¶
\[ \begin{align} f_1(t) &= e^{j(t + 15^\circ)} + e^{j(3t - 30^\circ)} \\ f_2(t) &= e^{j(t + 15^\circ)} + e^{j(6t + 60^\circ)} \\ f_3(t) &= e^{j(3t - 30^\circ)} + e^{j(6t + 60^\circ)} \end{align} \]
from itertools import combinations
plot_signals([
SignalInfo(
title=f'$\\omega_1$ = {omega1} rad/s, '
f'$\\phi_1$ = {np.round(np.degrees(phi1))}°\n'
f'$\\omega_2$ = {omega2} rad/s, '
f'$\\phi_2$ = {np.round(np.degrees(phi2))}°',
f=lambda t, omega1=omega1, phi1=phi1, omega2=omega2, phi2=phi2:
np.real(np.exp(1j * (omega1 * t + phi1)) + \
np.exp(1j * (omega2 * t + phi2)))
)
for ((omega1, phi1), (omega2, phi2)) in combinations(
zip(omega_values, phi_values), 2)
])
结论¶
实信号的幅值频谱是偶函数,相位频谱是奇函数。复信号的频谱没有这样的特点。